Article contents
Discrete quadratic estimates and holomorphic functional calculi in Banach spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
We develop a discrete version of the weak quadratic estimates for operators of type w explained by Cowling, Doust, McIntosh and Yagi, and show that analogous theorems hold. The method is direct and can be generalised to the case of finding necessary and sufficient conditions for an operator T to have a bounded functional calculus on a domain which touches σ(T) nontangentially at several points. For operators on Lp, 1 < p < ∞, it follows that T has a bounded functional calculus if and only if T satisfies discrete quadratic estimates. Using this, one easily obtains Albrecht's extension to a joint functional calculus for several commuting operators. In Hilbert space the methods show that an operator with a bounded functional calculus has a uniformly bounded matricial functional calculus.
The basic idea is to take a dyadic decomposition of the boundary of a sector Sv. Then on the kth ingerval consider an orthonormal sequence of polynomials 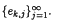 . For h ∈ H∞(Sν), estimates for the uniform norm of h on a smaller sector Sμ are obtained from the coefficients akj = (h, ek, j). These estimates are then used to prove the theorems.
. For h ∈ H∞(Sν), estimates for the uniform norm of h on a smaller sector Sμ are obtained from the coefficients akj = (h, ek, j). These estimates are then used to prove the theorems.
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 58 , Issue 2 , October 1998 , pp. 271 - 290
- Copyright
- Copyright © Australian Mathematical Society 1998
References
- 14
- Cited by

