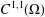Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Trudinger, Neil S.
2021.
On the local theory of prescribed Jacobian equations revisited.
Mathematics in Engineering,
Vol. 3,
Issue. 6,
p.
1.
Rankin, Cale
2021.
Strict convexity and $$C^1$$ regularity of solutions to generated Jacobian equations in dimension two.
Calculus of Variations and Partial Differential Equations,
Vol. 60,
Issue. 6,
Trudinger, Neil S.
2023.
A note on second derivative estimates for Monge-Ampère-type equations.
Advanced Nonlinear Studies,
Vol. 23,
Issue. 1,
Rankin, Cale
2023.
Strict g-Convexity for Generated Jacobian Equations with Applications to Global Regularity.
SIAM Journal on Mathematical Analysis,
Vol. 55,
Issue. 5,
p.
5685.
Jiang, Feida
2023.
Weak solutions of generated Jacobian equations.
Mathematics in Engineering,
Vol. 5,
Issue. 3,
p.
1.