Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T13:30:04.936Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS

Part of: Exponential sums and character sums Multiplicative number theory

Published online by Cambridge University Press:  01 March 2022

YAHUI YU  and
JIE WU Open the ORCID record for JIE WU [Opens in a new window]
YAHUI YU
Affiliation:
Department of Mathematics and Physics, Luoyang Institute of Science and Technology, Luoyang, Henan 471023, PR China e-mail: yuyahui@lit.edu.cn
JIE WU*
Affiliation:
CNRS UMR 8050, Laboratoire d’Analyse et de Mathématiques Appliquées, Université Paris-Est Créteil, 94010 Créteil Cedex, France
*
e-mail: jie.wu@u-pec.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 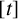$[t]$ be the integral part of the real number t. We study the distribution of the elements of the set 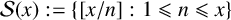$\mathcal {S}(x) := \{[{x}/{n}] : 1\leqslant n\leqslant x\}$ in the arithmetical progression 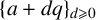$\{a+dq\}_{d\geqslant 0}$ . We give an asymptotic formula

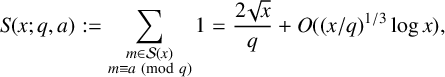$$ \begin{align*} S(x; q, a) := \sum_{\substack{m\in \mathcal{S}(x)\\ m\equiv a \pmod q}} 1 = \frac{2\sqrt{x}}{q} + O((x/q)^{1/3}\log x), \end{align*} $$

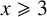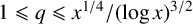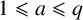which holds uniformly for $x\geqslant 3$ , $1\leqslant q\leqslant x^{1/4}/(\log x)^{3/2}$ and $1\leqslant a\leqslant q$ , where the implied constant is absolute. The special case 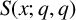$S(x; q, q)$ confirms a recent numerical test of Heyman [‘Cardinality of a floor function set’, Integers 19 (2019), Article no. A67].

Keywords

trigonometric and exponential sumsdistribution of integers in special residue classes

MSC classification

Primary: 11L03: Trigonometric and exponential sums, general
Secondary: 11N69: Distribution of integers in special residue classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 419 - 424
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is in part supported by the National Natural Science Foundation of China (Grant Nos. 11771211, 11971370 and 12071375), by the NSF of Chongqing (Grant No. cstc2019jcy-msxm1651) and by the Young Talent-training Plan for college teachers in Henan province (2019GGJS241).

References

Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums (Cambridge UniversityPress, Cambridge, 1991).CrossRefGoogle Scholar
Heyman, R., ‘Cardinality of a floor functionset’, Integers 19 (2019), Article no. A67.Google Scholar
Heyman, R., ‘Primes in floor function sets’, Preprint, 2021, arXiv:2111.00408v4[math.NT].Google Scholar
Ma, R. and Wu, J.,‘On the primes in floor function sets’, Preprint, 2021, arXiv:2112.12426v2 [math.NT].CrossRefGoogle Scholar