Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T13:47:44.727Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTION OF THE DIVISOR FUNCTION AT CONSECUTIVE INTEGERS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  09 September 2020

ELCHIN HASANALIZADE Open the ORCID record for ELCHIN HASANALIZADE [Opens in a new window]
ELCHIN HASANALIZADE*
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta, T1K 3M4, Canada
*
e-mail: e.hasanalizade@uleth.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we sharpen Hildebrand’s earlier result on a conjecture of Erdős on limit points of the sequence 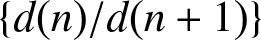${\{d(n)/d(n+1)\}}$ .

Keywords

divisor functionalmost primesErdős–Mirsky conjecture

MSC classification

Primary: 11N36: Applications of sieve methods
Secondary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 244 - 247
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Erdős, P., ‘Some problems on number theory’, Analytic and Elementary Number Theory (Marseille, 1983), Publications Mathématiques d’Orsay, 86 (Univ. Paris XI, Orsay, 1986), 53–67.Google Scholar
Erdős, P., Pomerance, C. and Sarközy, A., ‘On locally repeated values of certain arithmetic functions, II’, Acta Math. Hungar. 49 (1987), 251–259.CrossRefGoogle Scholar
Goldston, D. A., Graham, S., Pintz, J. and Yıldırım, C. Y., ‘Small gaps between products of two primes’, Proc. Lond. Math. Soc. 98(3) (2009), 741–774.CrossRefGoogle Scholar
Goldston, D. A., Graham, S., Pintz, J. and Yıldırım, C. Y., ‘Small gaps between almost primes, the parity problem and some conjectures of Erdös on consecutive integers’, Int. Math. Res. Not. IMRN 2011(7) (2011), 1439–1450.Google Scholar
Heath-Brown, D. R., ‘The divisor function at consecutive integers’, Mathematika 31 (1984), 141–149.CrossRefGoogle Scholar
Hildebrand, A. J., ‘The divisor function at consecutive integers’, Pacific J. Math. 129 (1987), 307–319.CrossRefGoogle Scholar
Kan, J. and Shan, Z., ‘On the divisor function $d(n)$’, Mathematika 43 (1996), 320–322.CrossRefGoogle Scholar
Kan, J. and Shan, Z., ‘On the divisor function $d(n)$, II’, Mathematika 46 (1999), 419–423.CrossRefGoogle Scholar
Spiro, C. A., For the Local Distribution of the Group-Counting Function, Orders Divisible by Fifth Powers Can Be Neglected, PhD Thesis, University of Illinois at Urbana-Champaign, 1981.Google Scholar