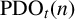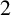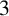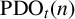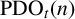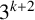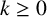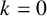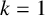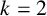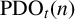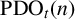1 Introduction and statement of results
A partition of a positive integer n is a nonincreasing sequence of positive integers, called parts, whose sum is n. In [Reference Andrews, Lewis and Lovejoy1], Andrews, Lewis and Lovejoy investigated the partition function
![]() $\text {PD}(n)$
which counts the number of partitions of n with designated summands. A partition of n with designated summands is obtained from an ordinary partition of n by tagging exactly one of each part size. For example,
$\text {PD}(n)$
which counts the number of partitions of n with designated summands. A partition of n with designated summands is obtained from an ordinary partition of n by tagging exactly one of each part size. For example,
![]() $\text {PD}(4)=10$
with the relevant partitions being
$\text {PD}(4)=10$
with the relevant partitions being
![]() $4', 3'+1', 2'+2, 2+2', 2'+1'+1, 2'+1+1', 1' +1+1+1, 1+1' +1+1, 1+1+1' +1, 1+1+1+1'$
. They also studied another partition function
$4', 3'+1', 2'+2, 2+2', 2'+1'+1, 2'+1+1', 1' +1+1+1, 1+1' +1+1, 1+1+1' +1, 1+1+1+1'$
. They also studied another partition function
![]() $\text {PDO}(n)$
which counts the number of partitions of n with designated summands in which all parts are odd. From the above example,
$\text {PDO}(n)$
which counts the number of partitions of n with designated summands in which all parts are odd. From the above example,
![]() $\text {PDO}(4)=5$
. Later, many authors have studied these two partition functions (see for example [Reference Baruah and Kaur2–Reference Chen, Ji, Jin and Shen4, Reference Xia17]).
$\text {PDO}(4)=5$
. Later, many authors have studied these two partition functions (see for example [Reference Baruah and Kaur2–Reference Chen, Ji, Jin and Shen4, Reference Xia17]).
Recently, Lin [Reference Lin9] introduced two new partition functions
![]() $\text {PD}_t(n)$
and
$\text {PD}_t(n)$
and
![]() $\text {PDO}_t(n)$
related to partitions with designated summands. The partition function
$\text {PDO}_t(n)$
related to partitions with designated summands. The partition function
![]() $\text {PD}_t(n)$
counts the total number of tagged parts over all the partitions of n with designated summands. For instance,
$\text {PD}_t(n)$
counts the total number of tagged parts over all the partitions of n with designated summands. For instance,
![]() $\text {PD}_t(4)=13$
. The other partition function
$\text {PD}_t(4)=13$
. The other partition function
![]() $\text {PDO}_t(n)$
counts the total number of tagged parts over all the partitions of n with designated summands in which all parts are odd. For example,
$\text {PDO}_t(n)$
counts the total number of tagged parts over all the partitions of n with designated summands in which all parts are odd. For example,
![]() $\text {PDO}_t(4)=6$
. Lin found the generating functions of
$\text {PDO}_t(4)=6$
. Lin found the generating functions of
![]() $\text {PD}_t(n)$
and
$\text {PD}_t(n)$
and
![]() $\text {PDO}_t(n)$
. The generating function of
$\text {PDO}_t(n)$
. The generating function of
![]() $\text {PDO}_t(n)$
is given by
$\text {PDO}_t(n)$
is given by
 $$ \begin{align} G(q):=\sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=\frac{qf_2f_3^2f_{12}^2}{f_1^2f_6}, \end{align} $$
$$ \begin{align} G(q):=\sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=\frac{qf_2f_3^2f_{12}^2}{f_1^2f_6}, \end{align} $$
where
![]() $f_k=\displaystyle (q^k; q^k)_{\infty }$
and
$f_k=\displaystyle (q^k; q^k)_{\infty }$
and
![]() $(a; q)_{\infty }:= \prod _{j=0}^{\infty }(1-aq^j)$
.
$(a; q)_{\infty }:= \prod _{j=0}^{\infty }(1-aq^j)$
.
Lin also established many congruences modulo small powers of 3 satisfied by
![]() $\text {PD}_t(n)$
and
$\text {PD}_t(n)$
and
![]() $\text {PDO}_t(n)$
. For example, he proved the following Ramanujan-type congruences modulo
$\text {PDO}_t(n)$
. For example, he proved the following Ramanujan-type congruences modulo
![]() $9$
and
$9$
and
![]() $27$
satisfied by
$27$
satisfied by
![]() $\text {PDO}_t(n)$
: for
$\text {PDO}_t(n)$
: for
![]() $n\geq 0$
,
$n\geq 0$
,
 $$ \begin{align*} \text{PDO}_t(8n)&\equiv \text{PDO}_t(12n)\equiv \text{PDO}_t(12n+8)\equiv 0 \pmod{9},\\ \text{PDO}_t(24n)&\equiv \text{PDO}_t(36n)\equiv \text{PDO}_t(36n+24)\equiv 0 \pmod{27}. \end{align*} $$
$$ \begin{align*} \text{PDO}_t(8n)&\equiv \text{PDO}_t(12n)\equiv \text{PDO}_t(12n+8)\equiv 0 \pmod{9},\\ \text{PDO}_t(24n)&\equiv \text{PDO}_t(36n)\equiv \text{PDO}_t(36n+24)\equiv 0 \pmod{27}. \end{align*} $$
He further conjectured the following congruences.
Conjecture 1.1 [Reference Lin9, Conjecture 6.1]
For
![]() $k,n\geq 0$
,
$k,n\geq 0$
,
 $$ \begin{align*} \mathrm{PDO}_t(8\cdot 3^k n)\equiv 0 \pmod{3^{k+2}}, \\ \mathrm{PDO}_t(12\cdot 3^k n)\equiv 0\pmod{3^{k+2}}. \end{align*} $$
$$ \begin{align*} \mathrm{PDO}_t(8\cdot 3^k n)\equiv 0 \pmod{3^{k+2}}, \\ \mathrm{PDO}_t(12\cdot 3^k n)\equiv 0\pmod{3^{k+2}}. \end{align*} $$
Lin proved Conjecture 1.1 for
![]() $k=0,1$
using basic q-series techniques. We prove the following theorem which establishes Conjecture 1.1 for
$k=0,1$
using basic q-series techniques. We prove the following theorem which establishes Conjecture 1.1 for
![]() $k=2$
.
$k=2$
.
Theorem 1.2. For all
![]() $n\geq 0$
,
$n\geq 0$
,
In addition to the study of Ramanujan-type congruences, it is an interesting problem to study the distribution of the partition function modulo positive integers M. To be precise, given an integral power series
![]() $F(q):=\sum _{n=0}^{\infty }a(n)q^n$
and
$F(q):=\sum _{n=0}^{\infty }a(n)q^n$
and
![]() $0\leq r<M$
, we define
$0\leq r<M$
, we define
An integral power series F is called lacunary modulo M if
that is, almost all of the coefficients of F are divisible by M.
It is a well-known fact that modular forms with integer Fourier coefficients are lacunary modulo any positive integer. Recently, in [Reference Cotron, Michaelsen, Stamm and Zhu5, Theorem 1.1], Cotron et al. extended this fact to integral weight eta-quotients modulo arbitrary powers of primes under certain strong conditions. In [Reference Lin9], Lin remarked that the generating function of
![]() $\text {PDO}_t(n)$
is a modular form. However, this observation is not quite correct because
$\text {PDO}_t(n)$
is a modular form. However, this observation is not quite correct because
![]() $\text {PDO}_t(n)$
is not holomorphic at the cusp 1. Also, the generating function of
$\text {PDO}_t(n)$
is not holomorphic at the cusp 1. Also, the generating function of
![]() $\text {PDO}_t(n)$
does not satisfy the conditions of [Reference Cotron, Michaelsen, Stamm and Zhu5, Theorem 1.1]. Therefore, it is an interesting problem to study the lacunarity of
$\text {PDO}_t(n)$
does not satisfy the conditions of [Reference Cotron, Michaelsen, Stamm and Zhu5, Theorem 1.1]. Therefore, it is an interesting problem to study the lacunarity of
![]() $G(q)=\sum _{n=0}^{\infty }\text {PDO}_t(n)q^n$
modulo arbitrary powers of primes. In the following theorem, we prove that
$G(q)=\sum _{n=0}^{\infty }\text {PDO}_t(n)q^n$
modulo arbitrary powers of primes. In the following theorem, we prove that
![]() $G(q)$
is lacunary modulo arbitrary powers of
$G(q)$
is lacunary modulo arbitrary powers of
![]() $2$
and
$2$
and
![]() $3$
.
$3$
.
Theorem 1.3. For any positive integer k,
Serre observed and Tate proved that the action of Hecke algebras on spaces of modular forms of level 1 modulo 2 is locally nilpotent (see for example [Reference Serre14–Reference Tate16]). Ono and Taguchi [Reference Ono and Taguchi13] showed that this phenomenon generalises to higher levels. We observe that, for any positive integer k, the generating function of
![]() $\text {PDO}_t(n)$
is congruent to an eta-quotient modulo
$\text {PDO}_t(n)$
is congruent to an eta-quotient modulo
![]() $2^k$
, and the eta-quotient is a modular form whose level is in Ono and Taguchi’s list. This allows us to use a result of Ono and Taguchi to prove the following congruence for
$2^k$
, and the eta-quotient is a modular form whose level is in Ono and Taguchi’s list. This allows us to use a result of Ono and Taguchi to prove the following congruence for
![]() $\text {PDO}_t(n)$
.
$\text {PDO}_t(n)$
.
Theorem 1.4. Let n be a nonnegative integer. Then there is an integer
![]() $s \geq 0$
such that for every
$s \geq 0$
such that for every
![]() $u \geq 1$
and distinct primes
$u \geq 1$
and distinct primes
![]() $p_1, \ldots , p_{s+u}$
coprime to
$p_1, \ldots , p_{s+u}$
coprime to
![]() $6$
,
$6$
,
whenever n is coprime to
![]() $p_1, \ldots , p_{s+u}$
.
$p_1, \ldots , p_{s+u}$
.
The rest of this paper is organised as follows. In Section 2, we recall some basic properties of modular forms and
![]() $\eta $
-quotients. In Section 3, we prove Theorem 1.2 using standard dissection of q-series. The proofs of Theorems 1.3 and 1.4 rely on properties of modular forms and we prove these theorems in Sections 4 and 5, respectively. Finding a proof of Conjecture 1.1 for
$\eta $
-quotients. In Section 3, we prove Theorem 1.2 using standard dissection of q-series. The proofs of Theorems 1.3 and 1.4 rely on properties of modular forms and we prove these theorems in Sections 4 and 5, respectively. Finding a proof of Conjecture 1.1 for
![]() $k\geq 3$
using standard dissection of q-series looks difficult. However, it might be possible to prove Conjecture 1.1 using modular forms.
$k\geq 3$
using standard dissection of q-series looks difficult. However, it might be possible to prove Conjecture 1.1 using modular forms.
2 Preliminaries
In this section, we recall some definitions and basic facts on modular forms and eta-quotients. For more details, see for example [Reference Koblitz8, Reference Ono12].
2.1 Spaces of modular forms
We first define the matrix groups
 $$ \begin{align*} \text{SL}_2(\mathbb{Z}) & :=\left\{\begin{bmatrix} a & b \\ c & d \end{bmatrix}: a, b, c, d \in \mathbb{Z}, ad-bc=1 \right\},\\ \Gamma_{0}(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : c\equiv 0\pmod N \right\}, \\ \Gamma_{1}(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \Gamma_0(N) : a\equiv d\equiv 1\pmod N \right\}, \end{align*} $$
$$ \begin{align*} \text{SL}_2(\mathbb{Z}) & :=\left\{\begin{bmatrix} a & b \\ c & d \end{bmatrix}: a, b, c, d \in \mathbb{Z}, ad-bc=1 \right\},\\ \Gamma_{0}(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : c\equiv 0\pmod N \right\}, \\ \Gamma_{1}(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \Gamma_0(N) : a\equiv d\equiv 1\pmod N \right\}, \end{align*} $$
and
 $$ \begin{align*}\Gamma(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a\equiv d\equiv 1\pmod N ~\text{and}~ b\equiv c\equiv 0\pmod N\right\}, \end{align*} $$
$$ \begin{align*}\Gamma(N) & :=\left\{ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \in \text{SL}_2(\mathbb{Z}) : a\equiv d\equiv 1\pmod N ~\text{and}~ b\equiv c\equiv 0\pmod N\right\}, \end{align*} $$
where N is a positive integer. A subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $\text {SL}_2(\mathbb {Z})$
is called a congruence subgroup if
$\text {SL}_2(\mathbb {Z})$
is called a congruence subgroup if
![]() $\Gamma (N)\subseteq \Gamma $
for some N. The smallest N such that
$\Gamma (N)\subseteq \Gamma $
for some N. The smallest N such that
![]() $\Gamma (N)\subseteq \Gamma $
is called the level of
$\Gamma (N)\subseteq \Gamma $
is called the level of
![]() $\Gamma $
. For example,
$\Gamma $
. For example,
![]() $\Gamma _0(N)$
and
$\Gamma _0(N)$
and
![]() $\Gamma _1(N)$
are congruence subgroups of level N.
$\Gamma _1(N)$
are congruence subgroups of level N.
Let
![]() $\mathbb {H}:=\{z\in \mathbb {C}: \text {Im}(z)>0\}$
be the upper half of the complex plane. The group
$\mathbb {H}:=\{z\in \mathbb {C}: \text {Im}(z)>0\}$
be the upper half of the complex plane. The group
 $$ \begin{align*}\text{GL}_2^{+}(\mathbb{R})=\left\{\begin{bmatrix} a & b \\ c & d \end{bmatrix}: a, b, c, d\in \mathbb{R}~\text{and}~ad-bc>0\right\}\end{align*} $$
$$ \begin{align*}\text{GL}_2^{+}(\mathbb{R})=\left\{\begin{bmatrix} a & b \\ c & d \end{bmatrix}: a, b, c, d\in \mathbb{R}~\text{and}~ad-bc>0\right\}\end{align*} $$
acts on
![]() $\mathbb {H}$
by
$\mathbb {H}$
by
 $$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} z=\displaystyle \frac{az+b}{cz+d}.\end{align*} $$
$$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} z=\displaystyle \frac{az+b}{cz+d}.\end{align*} $$
We identify
![]() $\infty $
with
$\infty $
with
![]() ${1}/{0}$
and define
${1}/{0}$
and define
 $$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \displaystyle\frac{r}{s}=\displaystyle \frac{ar+bs}{cr+ds},\end{align*} $$
$$ \begin{align*}\begin{bmatrix} a & b \\ c & d \end{bmatrix} \displaystyle\frac{r}{s}=\displaystyle \frac{ar+bs}{cr+ds},\end{align*} $$
where
![]() ${r}/{s}\in \mathbb {Q}\cup \{\infty \}$
. This gives an action of
${r}/{s}\in \mathbb {Q}\cup \{\infty \}$
. This gives an action of
![]() $\text {GL}_2^{+}(\mathbb {R})$
on the extended upper half-plane
$\text {GL}_2^{+}(\mathbb {R})$
on the extended upper half-plane
![]() $\mathbb {H}^{\ast }=\mathbb {H}\cup \mathbb {Q}\cup \{\infty \}$
. Suppose that
$\mathbb {H}^{\ast }=\mathbb {H}\cup \mathbb {Q}\cup \{\infty \}$
. Suppose that
![]() $\Gamma $
is a congruence subgroup of
$\Gamma $
is a congruence subgroup of
![]() $\text {SL}_2(\mathbb {Z})$
. A cusp of
$\text {SL}_2(\mathbb {Z})$
. A cusp of
![]() $\Gamma $
is an equivalence class in
$\Gamma $
is an equivalence class in
![]() $\mathbb {P}^1=\mathbb {Q}\cup \{\infty \}$
under the action of
$\mathbb {P}^1=\mathbb {Q}\cup \{\infty \}$
under the action of
![]() $\Gamma $
.
$\Gamma $
.
The group
![]() $\text {GL}_2^{+}(\mathbb {R})$
also acts on functions
$\text {GL}_2^{+}(\mathbb {R})$
also acts on functions
![]() $f: \mathbb {H}\rightarrow \mathbb {C}$
. In particular, suppose that
$f: \mathbb {H}\rightarrow \mathbb {C}$
. In particular, suppose that
![]() $\gamma =[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}]\in \text {GL}_2^{+}(\mathbb {R})$
. If
$\gamma =[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}]\in \text {GL}_2^{+}(\mathbb {R})$
. If
![]() $f(z)$
is a meromorphic function on
$f(z)$
is a meromorphic function on
![]() $\mathbb {H}$
and
$\mathbb {H}$
and
![]() $\ell $
is an integer, then define the slash operator
$\ell $
is an integer, then define the slash operator
![]() $|_{\ell }$
by
$|_{\ell }$
by
Definition 2.1. Let
![]() $\Gamma $
be a congruence subgroup of level N. A holomorphic function
$\Gamma $
be a congruence subgroup of level N. A holomorphic function
![]() $f: \mathbb {H}\rightarrow \mathbb {C}$
is called a modular form with integer weight
$f: \mathbb {H}\rightarrow \mathbb {C}$
is called a modular form with integer weight
![]() $\ell $
on
$\ell $
on
![]() $\Gamma $
if it satisfies the following conditions:
$\Gamma $
if it satisfies the following conditions:
-
(1)
 $f( ({az+b})/({cz+d}))=(cz+d)^{\ell }f(z)$
for all
$f( ({az+b})/({cz+d}))=(cz+d)^{\ell }f(z)$
for all
 $z\in \mathbb {H}$
and all
$z\in \mathbb {H}$
and all
 $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma $
;
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma $
; -
(2) if
 $\gamma \in \text {SL}_2(\mathbb {Z})$
, then
$\gamma \in \text {SL}_2(\mathbb {Z})$
, then
 $(f|_{\ell }\gamma )(z)$
has a Fourier expansion of the form
$(f|_{\ell }\gamma )(z)$
has a Fourier expansion of the form  $$ \begin{align*}(f|_{\ell}\gamma)(z)=\displaystyle\sum_{n\geq 0}a_{\gamma}(n)q_N^n,\end{align*} $$
$$ \begin{align*}(f|_{\ell}\gamma)(z)=\displaystyle\sum_{n\geq 0}a_{\gamma}(n)q_N^n,\end{align*} $$
where
 $q_N:=e^{2\pi iz/N}$
.
$q_N:=e^{2\pi iz/N}$
.
For a positive integer
![]() $\ell $
, the complex vector space of modular forms of weight
$\ell $
, the complex vector space of modular forms of weight
![]() $\ell $
with respect to a congruence subgroup
$\ell $
with respect to a congruence subgroup
![]() $\Gamma $
is denoted by
$\Gamma $
is denoted by
![]() $M_{\ell }(\Gamma )$
.
$M_{\ell }(\Gamma )$
.
Definition 2.2 [Reference Ono12, Definition 1.15]
If
![]() $\chi $
is a Dirichlet character modulo N, then we say that a modular form
$\chi $
is a Dirichlet character modulo N, then we say that a modular form
![]() $f\in M_{\ell }(\Gamma _1(N))$
has Nebentypus character
$f\in M_{\ell }(\Gamma _1(N))$
has Nebentypus character
![]() $\chi $
if
$\chi $
if
 $$ \begin{align*}f\left( \frac{az+b}{cz+d}\right)=\chi(d)(cz+d)^{\ell}f(z)\end{align*} $$
$$ \begin{align*}f\left( \frac{az+b}{cz+d}\right)=\chi(d)(cz+d)^{\ell}f(z)\end{align*} $$
for all
![]() $z\in \mathbb {H}$
and all
$z\in \mathbb {H}$
and all
![]() $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _0(N)$
. The space of such modular forms is denoted by
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _0(N)$
. The space of such modular forms is denoted by
![]() $M_{\ell }(\Gamma _0(N), \chi )$
.
$M_{\ell }(\Gamma _0(N), \chi )$
.
2.2 Modularity of eta-quotients
The relevant modular forms in this paper are those that arise from eta-quotients. Recall that the Dedekind eta-function
![]() $\eta (z)$
is defined by
$\eta (z)$
is defined by
 $$ \begin{align*} \eta(z):=q^{1/24}(q;q)_{\infty}=q^{1/24}\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
$$ \begin{align*} \eta(z):=q^{1/24}(q;q)_{\infty}=q^{1/24}\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$
where
![]() $q:=e^{2\pi iz}$
and
$q:=e^{2\pi iz}$
and
![]() $z\in \mathbb {H}$
. A function
$z\in \mathbb {H}$
. A function
![]() $f(z)$
is called an eta-quotient if it is of the form
$f(z)$
is called an eta-quotient if it is of the form
 $$ \begin{align*} f(z)=\prod_{\delta\mid N}\eta(\delta z)^{r_{\delta}}, \end{align*} $$
$$ \begin{align*} f(z)=\prod_{\delta\mid N}\eta(\delta z)^{r_{\delta}}, \end{align*} $$
where N is a positive integer and
![]() $r_{\delta }$
is an integer.
$r_{\delta }$
is an integer.
We now recall two theorems from [Reference Ono12, page 18] on modularity of eta-quotients. We will use these two results to verify modularity of certain eta-quotients appearing in the proofs of our main results.
Theorem 2.3 [Reference Ono12, Theorem 1.64]
If
![]() $f(z)=\prod _{\delta \mid N}\eta (\delta z)^{r_{\delta }}$
is an eta-quotient such that
$f(z)=\prod _{\delta \mid N}\eta (\delta z)^{r_{\delta }}$
is an eta-quotient such that
![]() $\ell =\tfrac 12\sum _{\delta \mid N}r_{\delta }\in \mathbb {Z}$
,
$\ell =\tfrac 12\sum _{\delta \mid N}r_{\delta }\in \mathbb {Z}$
,
 $$ \begin{align*}\sum_{\delta\mid N} \delta r_{\delta}\equiv 0 \pmod{24}\end{align*} $$
$$ \begin{align*}\sum_{\delta\mid N} \delta r_{\delta}\equiv 0 \pmod{24}\end{align*} $$
and
 $$ \begin{align*}\sum_{\delta\mid N} \frac{N}{\delta}r_{\delta}\equiv 0 \pmod{24},\end{align*} $$
$$ \begin{align*}\sum_{\delta\mid N} \frac{N}{\delta}r_{\delta}\equiv 0 \pmod{24},\end{align*} $$
then
![]() $f(z)$
satisfies
$f(z)$
satisfies
 $$ \begin{align*}f\left( \frac{az+b}{cz+d}\right)=\chi(d)(cz+d)^{\ell}f(z)\end{align*} $$
$$ \begin{align*}f\left( \frac{az+b}{cz+d}\right)=\chi(d)(cz+d)^{\ell}f(z)\end{align*} $$
for every
![]() $[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _0(N)$
. Here, the character
$[\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}] \in \Gamma _0(N)$
. Here, the character
![]() $\chi $
is defined by
$\chi $
is defined by
![]() $\chi (d):=\big(\frac{(-1)^\ell s}{d}\big)$
, where
$\chi (d):=\big(\frac{(-1)^\ell s}{d}\big)$
, where
![]() $s:= \prod _{\delta \mid N}\delta ^{r_{\delta }}$
.
$s:= \prod _{\delta \mid N}\delta ^{r_{\delta }}$
.
Suppose that f is an eta-quotient satisfying the conditions of Theorem 2.3 and that the associated weight
![]() $\ell $
is a positive integer. If
$\ell $
is a positive integer. If
![]() $f(z)$
is holomorphic at all of the cusps of
$f(z)$
is holomorphic at all of the cusps of
![]() $\Gamma _0(N)$
, then
$\Gamma _0(N)$
, then
![]() $f(z)\in M_{\ell }(\Gamma _0(N), \chi )$
. The following theorem gives the necessary criterion for determining orders of an eta-quotient at cusps.
$f(z)\in M_{\ell }(\Gamma _0(N), \chi )$
. The following theorem gives the necessary criterion for determining orders of an eta-quotient at cusps.
Theorem 2.4 [Reference Ono12, Theorem 1.65]
Let
![]() $c, d$
and N be positive integers with
$c, d$
and N be positive integers with
![]() $d\mid N$
and
$d\mid N$
and
![]() $\gcd (c, d)=1$
. If f is an eta-quotient satisfying the conditions of Theorem 2.3 for N, then the order of vanishing of
$\gcd (c, d)=1$
. If f is an eta-quotient satisfying the conditions of Theorem 2.3 for N, then the order of vanishing of
![]() $f(z)$
at the cusp
$f(z)$
at the cusp
![]() ${c}/{d}$
is
${c}/{d}$
is
 $$ \begin{align*}\frac{N}{24}\sum_{\delta\mid N}\frac{\gcd(d,\delta)^2r_{\delta}}{\gcd(d,{N}/{d})d\delta}.\end{align*} $$
$$ \begin{align*}\frac{N}{24}\sum_{\delta\mid N}\frac{\gcd(d,\delta)^2r_{\delta}}{\gcd(d,{N}/{d})d\delta}.\end{align*} $$
Finally, we recall the definition of Hecke operators. Let m be a positive integer and
![]() $f(z) = \sum _{n=0}^{\infty } a(n)q^n \in M_{\ell }(\Gamma _0(N),\chi )$
. Then, the action of the Hecke operator
$f(z) = \sum _{n=0}^{\infty } a(n)q^n \in M_{\ell }(\Gamma _0(N),\chi )$
. Then, the action of the Hecke operator
![]() $T_m$
on
$T_m$
on
![]() $f(z)$
is defined by
$f(z)$
is defined by
 $$ \begin{align*} f(z)|T_m := \sum_{n=0}^{\infty} \bigg(\sum_{d\mid \gcd(n,m)}\chi(d)d^{\ell-1}a\bigg(\frac{nm}{d^2}\bigg)\bigg)q^n. \end{align*} $$
$$ \begin{align*} f(z)|T_m := \sum_{n=0}^{\infty} \bigg(\sum_{d\mid \gcd(n,m)}\chi(d)d^{\ell-1}a\bigg(\frac{nm}{d^2}\bigg)\bigg)q^n. \end{align*} $$
In particular, if
![]() $m=p$
is prime,
$m=p$
is prime,
 $$ \begin{align*} f(z)|T_p := \sum_{n=0}^{\infty} \bigg(a(pn)+\chi(p)p^{\ell-1}a\bigg(\frac{n}{p}\bigg)\bigg)q^n. \end{align*} $$
$$ \begin{align*} f(z)|T_p := \sum_{n=0}^{\infty} \bigg(a(pn)+\chi(p)p^{\ell-1}a\bigg(\frac{n}{p}\bigg)\bigg)q^n. \end{align*} $$
We adopt the convention that
![]() $a(n)=0$
unless n is a nonnegative integer.
$a(n)=0$
unless n is a nonnegative integer.
3 Proof of Theorem 1.2
To prove Theorem 1.2, we need the following lemma.
Lemma 3.1. The following identities hold:
 $$ \begin{align*} \frac{f_3}{{f}^3_1}&=\frac{{f}^6_4{f}^3_6}{{f}^9_2{f}^2_{12}}+3q\frac{{f}^2_4f_6{f}^2_{12}}{{f}^7_2},\\ \frac{1}{{f}^4_1}&=\frac{{f}^{14}_4}{{f}^{14}_2{f}^4_8}+4q\frac{{f}^2_4{f}^4_8}{{f}^{10}_2},\\ \frac{f_2}{{f}^2_1}&=\frac{{f}^4_6{f}^6_9}{{f}^8_3{f}^3_{18}}+2q\frac{{f}^3_6{f}^3_9}{{f}^7_3}+4q^2\frac{{f}^2_6{f}^3_{18}}{{f}^6_3},\\ f_1f_2&=\frac{f_6{f}^4_9}{f_3{f}^2_{18}}-qf_9f_{18}-2q^2\frac{f_3{f}^4_{18}}{f_6{f}^2_9},\\ {f}^3_1&=\frac{f_6{f}^6_9}{f_3{f}^3_{18}}-3q{f}^3_9+4q^3\frac{{f}^2_3{f}^6_{18}}{{f}^2_6{f}^3_9}. \end{align*} $$
$$ \begin{align*} \frac{f_3}{{f}^3_1}&=\frac{{f}^6_4{f}^3_6}{{f}^9_2{f}^2_{12}}+3q\frac{{f}^2_4f_6{f}^2_{12}}{{f}^7_2},\\ \frac{1}{{f}^4_1}&=\frac{{f}^{14}_4}{{f}^{14}_2{f}^4_8}+4q\frac{{f}^2_4{f}^4_8}{{f}^{10}_2},\\ \frac{f_2}{{f}^2_1}&=\frac{{f}^4_6{f}^6_9}{{f}^8_3{f}^3_{18}}+2q\frac{{f}^3_6{f}^3_9}{{f}^7_3}+4q^2\frac{{f}^2_6{f}^3_{18}}{{f}^6_3},\\ f_1f_2&=\frac{f_6{f}^4_9}{f_3{f}^2_{18}}-qf_9f_{18}-2q^2\frac{f_3{f}^4_{18}}{f_6{f}^2_9},\\ {f}^3_1&=\frac{f_6{f}^6_9}{f_3{f}^3_{18}}-3q{f}^3_9+4q^3\frac{{f}^2_3{f}^6_{18}}{{f}^2_6{f}^3_9}. \end{align*} $$
Proof. For the proof of first identity, see [Reference Naika and Gireesh10]. The second identity is proved in [Reference da Silva and Sellers6]. The remaining three identities of the lemma are proved in [Reference Hirschhorn7].
Proof of Theorem 1.2
By (1.1), we have
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=q\frac{f_2{f}^2_3{f}^2_{12}}{{f}^2_1f_6}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=q\frac{f_2{f}^2_3{f}^2_{12}}{{f}^2_1f_6}. \end{align*} $$
Substituting the 3-dissection formula for
![]() ${f_2}/{{f}^2_1}$
from Lemma 3.1,
${f_2}/{{f}^2_1}$
from Lemma 3.1,
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=q\frac{{f}^2_3{f}^2_{12}}{f_6}\bigg( \frac{{f}^4_6{f}^6_9}{{f}^8_3{f}^3_{18}}+2q\frac{{f}^3_6{f}^3_9}{{f}^7_3}+4q^2\frac{{f}^2_6{f}^3_{18}}{{f}^6_3}\bigg). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n=q\frac{{f}^2_3{f}^2_{12}}{f_6}\bigg( \frac{{f}^4_6{f}^6_9}{{f}^8_3{f}^3_{18}}+2q\frac{{f}^3_6{f}^3_9}{{f}^7_3}+4q^2\frac{{f}^2_6{f}^3_{18}}{{f}^6_3}\bigg). \end{align*} $$
Extracting those terms of the form
![]() $q^{3n}$
on both sides of this equation and replacing
$q^{3n}$
on both sides of this equation and replacing
![]() $q^3$
by q, we find that
$q^3$
by q, we find that
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(3n)q^n=4q\frac{f_2{f}^2_4{f}^3_6}{{f}^4_1}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(3n)q^n=4q\frac{f_2{f}^2_4{f}^3_6}{{f}^4_1}. \end{align*} $$
Substituting the 2-dissection formula for
![]() ${1}/{{f}^4_1}$
from Lemma 3.1 yields
${1}/{{f}^4_1}$
from Lemma 3.1 yields
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(3n)q^n=4qf_2{f}^2_4{f}^3_6\bigg(\frac{{f}^{14}_4}{{f}^{14}_2{f}^4_8}+4q\frac{{f}^2_4{f}^4_8}{{f}^{10}_2} \bigg). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(3n)q^n=4qf_2{f}^2_4{f}^3_6\bigg(\frac{{f}^{14}_4}{{f}^{14}_2{f}^4_8}+4q\frac{{f}^2_4{f}^4_8}{{f}^{10}_2} \bigg). \end{align*} $$
Extracting those terms of the form
![]() $q^{2n}$
on both sides of this equation and replacing
$q^{2n}$
on both sides of this equation and replacing
![]() $q^2$
by q,
$q^2$
by q,
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(6n)q^n=16q{f}^4_2{f}^4_4\bigg( \frac{f_3}{{f}^3_1}\bigg)^3. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(6n)q^n=16q{f}^4_2{f}^4_4\bigg( \frac{f_3}{{f}^3_1}\bigg)^3. \end{align*} $$
Substituting the 2-dissection formula for
![]() ${f_3}/{{f}^3_1}$
from Lemma 3.1 yields
${f_3}/{{f}^3_1}$
from Lemma 3.1 yields
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(6n)q^n & =16q\frac{{f}^{22}_4{f}^9_6}{{f}^{23}_2{f}^6_{12}}+16\cdot9q^2\frac{{f}^{18}_4{f}^7_6}{{f}^{21}_2{f}^2_{12}}+16\cdot27q^3\frac{{f}^{14}_4{f}^5_6{f}^2_{12}}{{f}^{19}_2} \\ &\quad +16\cdot27q^4\frac{{f}^{10}_4{f}^3_6{f}^6_{12}}{{f}^{17}_2}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(6n)q^n & =16q\frac{{f}^{22}_4{f}^9_6}{{f}^{23}_2{f}^6_{12}}+16\cdot9q^2\frac{{f}^{18}_4{f}^7_6}{{f}^{21}_2{f}^2_{12}}+16\cdot27q^3\frac{{f}^{14}_4{f}^5_6{f}^2_{12}}{{f}^{19}_2} \\ &\quad +16\cdot27q^4\frac{{f}^{10}_4{f}^3_6{f}^6_{12}}{{f}^{17}_2}. \end{align*} $$
Extracting those terms of the form
![]() $q^{2n}$
on both sides of this equation and replacing
$q^{2n}$
on both sides of this equation and replacing
![]() $q^2$
by q,
$q^2$
by q,
 $$ \begin{align} \sum_{n=0}^{\infty}\text{PDO}_t(12n)q^n=16\cdot9q\frac{{f}^{18}_2{f}^7_3}{{f}^{21}_1{f}^2_6}+16\cdot27q^2\frac{{f}^{10}_2{f}^3_3{f}^6_6}{{f}^{17}_1}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}\text{PDO}_t(12n)q^n=16\cdot9q\frac{{f}^{18}_2{f}^7_3}{{f}^{21}_1{f}^2_6}+16\cdot27q^2\frac{{f}^{10}_2{f}^3_3{f}^6_6}{{f}^{17}_1}. \end{align} $$
By the binomial theorem,
 $$ \begin{align*} \frac{{f}^{10}_2}{{f}^{17}_1}\equiv\frac{{f}^{9}_2}{{f}^{18}_1}f_1f_2\equiv\frac{{f}^{3}_6}{{f}^{6}_3}f_1f_2 \pmod{3}. \end{align*} $$
$$ \begin{align*} \frac{{f}^{10}_2}{{f}^{17}_1}\equiv\frac{{f}^{9}_2}{{f}^{18}_1}f_1f_2\equiv\frac{{f}^{3}_6}{{f}^{6}_3}f_1f_2 \pmod{3}. \end{align*} $$
Substituting the 3-dissection formula for
![]() $f_1f_2$
from Lemma 3.1,
$f_1f_2$
from Lemma 3.1,
 $$ \begin{align} \frac{{f}^{10}_2}{{f}^{17}_1}\equiv\frac{{f}^{4}_6{f}^4_9}{{f}^7_3{f}^2_{18}}-q\frac{{f}^3_6f_9f_{18}}{{f}^6_3}-2q^2\frac{{f}^2_6{f}^4_{18}}{{f}^5_3{f}^2_9} \pmod{3}. \end{align} $$
$$ \begin{align} \frac{{f}^{10}_2}{{f}^{17}_1}\equiv\frac{{f}^{4}_6{f}^4_9}{{f}^7_3{f}^2_{18}}-q\frac{{f}^3_6f_9f_{18}}{{f}^6_3}-2q^2\frac{{f}^2_6{f}^4_{18}}{{f}^5_3{f}^2_9} \pmod{3}. \end{align} $$
Again, using the binomial theorem,
 $$ \begin{align*} \frac{{f}^{18}_2}{{f}^{21}_1}\equiv\frac{{f}^{18}_2}{{f}^{27}_1}{f}^6_1\equiv\frac{{f}^{6}_6}{{f}^{9}_3}( {f}^3_1) ^2 \pmod{9}. \end{align*} $$
$$ \begin{align*} \frac{{f}^{18}_2}{{f}^{21}_1}\equiv\frac{{f}^{18}_2}{{f}^{27}_1}{f}^6_1\equiv\frac{{f}^{6}_6}{{f}^{9}_3}( {f}^3_1) ^2 \pmod{9}. \end{align*} $$
Substituting the 3-dissection formula for
![]() ${f}^3_1$
from Lemma 3.1,
${f}^3_1$
from Lemma 3.1,
 $$ \begin{align} \frac{{f}^{18}_2}{{f}^{21}_1}&\equiv\frac{{f}^8_6{f}^{12}_9}{{f}^{11}_3{f}^6_{18}}-6q\frac{{f}^7_6{f}^9_9}{{f}^{10}_3{f}^3_{18}}+9q^2\frac{{f}^6_6{f}^6_9}{{f}^9_3}+8q^3\frac{{f}^5_6{f}^3_9{f}^3_{18}}{{f}^{8}_3}-24q^4\frac{{f}^4_6{f}^6_{18}}{{f}^7_3}\notag \\ &\quad +16q^6\frac{{f}^2_6{f}^{12}_{18}}{{f}^5_3{f}^6_9} \pmod{9}. \end{align} $$
$$ \begin{align} \frac{{f}^{18}_2}{{f}^{21}_1}&\equiv\frac{{f}^8_6{f}^{12}_9}{{f}^{11}_3{f}^6_{18}}-6q\frac{{f}^7_6{f}^9_9}{{f}^{10}_3{f}^3_{18}}+9q^2\frac{{f}^6_6{f}^6_9}{{f}^9_3}+8q^3\frac{{f}^5_6{f}^3_9{f}^3_{18}}{{f}^{8}_3}-24q^4\frac{{f}^4_6{f}^6_{18}}{{f}^7_3}\notag \\ &\quad +16q^6\frac{{f}^2_6{f}^{12}_{18}}{{f}^5_3{f}^6_9} \pmod{9}. \end{align} $$
Substituting (3.2) and (3.3) in (3.1), and then extracting the terms of the form
![]() $q^{3n}$
on both sides, we find that
$q^{3n}$
on both sides, we find that
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^{3n}\equiv16\cdot81q^3\frac{{f}^4_6{f}^6_9}{{f}^2_3}-16\cdot27q^3\frac{{f}^9_6f_9f_{18}}{{f}^3_3}\pmod{81}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^{3n}\equiv16\cdot81q^3\frac{{f}^4_6{f}^6_9}{{f}^2_3}-16\cdot27q^3\frac{{f}^9_6f_9f_{18}}{{f}^3_3}\pmod{81}. \end{align*} $$
Replacing
![]() $q^3$
by q, and then substituting the 2-dissection formula for
$q^3$
by q, and then substituting the 2-dissection formula for
![]() ${f_3}/{{f}^3_1}$
from Lemma 3.1,
${f_3}/{{f}^3_1}$
from Lemma 3.1,
 $$ \begin{align} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^n&\equiv-16\cdot27q\frac{{f}^9_2f_3f_6}{{f}^3_1} \pmod{81}\qquad\qquad\qquad\qquad \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^n&\equiv-16\cdot27q\frac{{f}^9_2f_3f_6}{{f}^3_1} \pmod{81}\qquad\qquad\qquad\qquad \end{align} $$
 $$ \begin{align} &\qquad\ \ \,\kern1pt\qquad\qquad\equiv-16\cdot27q{f}^9_2f_6\frac{f_3}{{f}^3_1} \pmod{81}\nonumber\\ &\qquad\ \ \,\kern1pt\qquad\qquad\equiv-16\cdot27q\frac{{f}^6_4{f}^4_6}{{f}^2_{12}}-16\cdot81q^2{f}^2_2{f}^2_4{f}^2_6{f}^2_{12} \pmod{81}\nonumber\\ &\qquad\ \ \,\kern1pt\qquad\qquad\equiv -16\cdot27q\frac{{f}^6_4{f}^4_6}{{f}^2_{12}} \pmod{81}. \end{align} $$
$$ \begin{align} &\qquad\ \ \,\kern1pt\qquad\qquad\equiv-16\cdot27q{f}^9_2f_6\frac{f_3}{{f}^3_1} \pmod{81}\nonumber\\ &\qquad\ \ \,\kern1pt\qquad\qquad\equiv-16\cdot27q\frac{{f}^6_4{f}^4_6}{{f}^2_{12}}-16\cdot81q^2{f}^2_2{f}^2_4{f}^2_6{f}^2_{12} \pmod{81}\nonumber\\ &\qquad\ \ \,\kern1pt\qquad\qquad\equiv -16\cdot27q\frac{{f}^6_4{f}^4_6}{{f}^2_{12}} \pmod{81}. \end{align} $$
Extracting the terms of the form
![]() $q^{2n}$
on both sides of (3.5),
$q^{2n}$
on both sides of (3.5),
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(72n)q^{2n}&\equiv0 \pmod{81}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(72n)q^{2n}&\equiv0 \pmod{81}. \end{align*} $$
This completes the proof of (1.2).
We next prove (1.3). By the binomial theorem,
 $$ \begin{align} \frac{{f}^9_2}{{f}^3_1}\equiv\frac{{f}^3_6}{f_3} \pmod{3}. \end{align} $$
$$ \begin{align} \frac{{f}^9_2}{{f}^3_1}\equiv\frac{{f}^3_6}{f_3} \pmod{3}. \end{align} $$
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^n\equiv-16\cdot27q{f}^4_6 \pmod{81}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(36n)q^n\equiv-16\cdot27q{f}^4_6 \pmod{81}. \end{align*} $$
Extracting the terms of the form
![]() $q^{3n}$
on both sides yields
$q^{3n}$
on both sides yields
 $$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(108n)q^{3n}\equiv0 \pmod{81}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{\infty}\text{PDO}_t(108n)q^{3n}\equiv0 \pmod{81}. \end{align*} $$
This completes the proof of (1.3).
4 Proof of Theorem 1.3
Given a prime p, let
 $$ \begin{align*} A_p(z) = \prod_{n=1}^{\infty} \frac{(1-q^{n})^p}{(1-q^{pn})} = \frac{\eta^p(z)}{\eta(pz)}. \end{align*} $$
$$ \begin{align*} A_p(z) = \prod_{n=1}^{\infty} \frac{(1-q^{n})^p}{(1-q^{pn})} = \frac{\eta^p(z)}{\eta(pz)}. \end{align*} $$
Then, using the binomial theorem,
 $$ \begin{align*} A_p^{p^k}(z) = \frac{\eta^{p^{k+1}}(z)}{\eta^{p^k}(pz)} \equiv 1 \pmod {p^{k+1}}. \end{align*} $$
$$ \begin{align*} A_p^{p^k}(z) = \frac{\eta^{p^{k+1}}(z)}{\eta^{p^k}(pz)} \equiv 1 \pmod {p^{k+1}}. \end{align*} $$
Define
![]() $B_{p,k}(z)$
by
$B_{p,k}(z)$
by
 $$ \begin{align} B_{p,k}(z) = \bigg(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\bigg)A_p^{p^k}(z). \end{align} $$
$$ \begin{align} B_{p,k}(z) = \bigg(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\bigg)A_p^{p^k}(z). \end{align} $$
Modulo
![]() $p^{k+1}$
,
$p^{k+1}$
,
 $$ \begin{align} B_{p,k}(z) \equiv \frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)} = \frac{qf_2f_3^2f_{12}^2}{f_1^2f_6}. \end{align} $$
$$ \begin{align} B_{p,k}(z) \equiv \frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)} = \frac{qf_2f_3^2f_{12}^2}{f_1^2f_6}. \end{align} $$
 $$ \begin{align} B_{p,k}(z) \equiv \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n \pmod {p^{k+1}}. \end{align} $$
$$ \begin{align} B_{p,k}(z) \equiv \sum_{n=0}^{\infty}\text{PDO}_t(n)q^n \pmod {p^{k+1}}. \end{align} $$
Proof of Theorem 1.3
We put
![]() $p=2$
in (4.1) to obtain
$p=2$
in (4.1) to obtain
 $$ \begin{align*} B_{2,k}(z) = \left(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\right)A_2^{2^k}(z)=\frac{\eta(2z)^{1-2^{k}}\eta(3z)^2\eta(12z)^2\eta(z)^{2^{k+1}-2}}{\eta(6z)}. \end{align*} $$
$$ \begin{align*} B_{2,k}(z) = \left(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\right)A_2^{2^k}(z)=\frac{\eta(2z)^{1-2^{k}}\eta(3z)^2\eta(12z)^2\eta(z)^{2^{k+1}-2}}{\eta(6z)}. \end{align*} $$
Now,
![]() $B_{2, k}$
is an eta-quotient with level
$B_{2, k}$
is an eta-quotient with level
![]() $N=144$
. The cusps of
$N=144$
. The cusps of
![]() $\Gamma _{0}(144)$
are represented by fractions
$\Gamma _{0}(144)$
are represented by fractions
![]() ${c}/{d}$
, where
${c}/{d}$
, where
![]() $d\mid 144$
and
$d\mid 144$
and
![]() $\gcd (c, d)=1$
(see for example [Reference Ono11, page 5]). By Theorem 2.4,
$\gcd (c, d)=1$
(see for example [Reference Ono11, page 5]). By Theorem 2.4,
![]() $B_{2,k}(z)$
is holomorphic at a cusp
$B_{2,k}(z)$
is holomorphic at a cusp
![]() ${c}/{d}$
if and only if
${c}/{d}$
if and only if
 $$ \begin{align*} S&:=12\frac{\gcd(d,1)^2}{\gcd(d,12)^2} (2^{k+1}-2)+ 6\frac{\gcd(d,2)^2}{\gcd(d,12)^2}(1-2^k )+8\frac{\gcd(d,3)^2}{\gcd(d,12)^2} \\ & \quad -2\frac{\gcd(d,6)^2}{\gcd(d,12)^2}+2 \geq 0. \end{align*} $$
$$ \begin{align*} S&:=12\frac{\gcd(d,1)^2}{\gcd(d,12)^2} (2^{k+1}-2)+ 6\frac{\gcd(d,2)^2}{\gcd(d,12)^2}(1-2^k )+8\frac{\gcd(d,3)^2}{\gcd(d,12)^2} \\ & \quad -2\frac{\gcd(d,6)^2}{\gcd(d,12)^2}+2 \geq 0. \end{align*} $$
To find all the possible values of S, we prepared Table 1 using MATLAB. Using Table 1, we find that
![]() $S\geq 0$
for all
$S\geq 0$
for all
![]() $d\mid 144$
. Hence,
$d\mid 144$
. Hence,
![]() $B_{2,k}(z)$
is holomorphic at every cusp
$B_{2,k}(z)$
is holomorphic at every cusp
![]() ${c}/{d}$
. From Theorem 2.3, the weight of
${c}/{d}$
. From Theorem 2.3, the weight of
![]() $B_{2,k}(z)$
is
$B_{2,k}(z)$
is
![]() $\ell =2^{k-1}+1$
. Also, the associated character for
$\ell =2^{k-1}+1$
. Also, the associated character for
![]() $B_{2,k}(z)$
is given by
$B_{2,k}(z)$
is given by
 $$ \begin{align*} \chi_1=\bigg(\frac{(-1)^{2^{k-1}+1}2^{4- 2^{k}}3^{3}}{\bullet}\bigg). \end{align*} $$
$$ \begin{align*} \chi_1=\bigg(\frac{(-1)^{2^{k-1}+1}2^{4- 2^{k}}3^{3}}{\bullet}\bigg). \end{align*} $$
Finally, by Theorem 2.3,
![]() $B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
for
$B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
for
![]() $k\geq 1$
. Given any positive integer m, by a deep theorem of Serre [Reference Ono12, page 43], if
$k\geq 1$
. Given any positive integer m, by a deep theorem of Serre [Reference Ono12, page 43], if
![]() $f(z)\in M_{\ell }(\Gamma _0(N), \chi )$
has the Fourier expansion
$f(z)\in M_{\ell }(\Gamma _0(N), \chi )$
has the Fourier expansion
 $$ \begin{align*} f(z)=\sum_{n=0}^{\infty}c(n)q^n\in \mathbb{Z}[[q]], \end{align*} $$
$$ \begin{align*} f(z)=\sum_{n=0}^{\infty}c(n)q^n\in \mathbb{Z}[[q]], \end{align*} $$
then there is a constant
![]() $\alpha>0$
such that
$\alpha>0$
such that
 $$ \begin{align*} \# \{n\leq X: c(n)\not\equiv 0 \pmod{m} \}= \mathcal{O}\bigg(\frac{X}{(\log{}X)^{\alpha}}\bigg). \end{align*} $$
$$ \begin{align*} \# \{n\leq X: c(n)\not\equiv 0 \pmod{m} \}= \mathcal{O}\bigg(\frac{X}{(\log{}X)^{\alpha}}\bigg). \end{align*} $$
This yields
Since
![]() $B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
, the Fourier coefficients of
$B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
, the Fourier coefficients of
![]() $B_{2,k}(z)$
are almost always divisible by
$B_{2,k}(z)$
are almost always divisible by
![]() $m=2^k$
. Now, using (4.3) completes the proof of (1.4).
$m=2^k$
. Now, using (4.3) completes the proof of (1.4).
Table 1 Data to find the values of
![]() $S$
.
$S$
.

We next prove (1.5). We put
![]() $p=3$
in (4.1) to obtain
$p=3$
in (4.1) to obtain
 $$ \begin{align*} B_{3,k}(z) = \bigg(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\bigg)\,A_3^{3^k}(z)=\frac{\eta(2z)\eta(3z)^{2-3^{k}}\eta(12z)^2\eta(z)^{3^{k+1}-2}}{\eta(6z)}. \end{align*} $$
$$ \begin{align*} B_{3,k}(z) = \bigg(\frac{\eta(2z)\eta(3z)^2\eta(12z)^2}{\eta(z)^2\eta(6z)}\bigg)\,A_3^{3^k}(z)=\frac{\eta(2z)\eta(3z)^{2-3^{k}}\eta(12z)^2\eta(z)^{3^{k+1}-2}}{\eta(6z)}. \end{align*} $$
Now,
![]() $B_{3, k}$
is an eta-quotient with
$B_{3, k}$
is an eta-quotient with
![]() $N=144$
. As before, the cusps of
$N=144$
. As before, the cusps of
![]() $\Gamma _{0}(144)$
are represented by fractions
$\Gamma _{0}(144)$
are represented by fractions
![]() ${c}/{d}$
, where
${c}/{d}$
, where
![]() $d\mid 144$
and
$d\mid 144$
and
![]() $\gcd (c, d)=1$
. By Theorem 2.4,
$\gcd (c, d)=1$
. By Theorem 2.4,
![]() $B_{3,k}(z)$
is holomorphic at a cusp
$B_{3,k}(z)$
is holomorphic at a cusp
![]() ${c}/{d}$
if and only if
${c}/{d}$
if and only if
 $$ \begin{align*} L:= &~12\frac{\gcd(d,1)^2}{\gcd(d,12)^2} (3^{k+1}-2)+4\frac{\gcd(d,3)^2}{\gcd(d,12)^2}(2-3^k) + 6\frac{\gcd(d,2)^2}{\gcd(d,12)^2}\\ &-2\frac{\gcd(d,6)^2}{\gcd(d,12)^2}+2 \geq 0. \end{align*} $$
$$ \begin{align*} L:= &~12\frac{\gcd(d,1)^2}{\gcd(d,12)^2} (3^{k+1}-2)+4\frac{\gcd(d,3)^2}{\gcd(d,12)^2}(2-3^k) + 6\frac{\gcd(d,2)^2}{\gcd(d,12)^2}\\ &-2\frac{\gcd(d,6)^2}{\gcd(d,12)^2}+2 \geq 0. \end{align*} $$
From Table 1,
![]() $L\geq 0$
for all
$L\geq 0$
for all
![]() $d\mid 144$
. By Theorem 2.3,
$d\mid 144$
. By Theorem 2.3,
![]() $B_{3,k}(z) \in M_{3^{k}+1}(\Gamma _{0}(144), \chi _2)$
, where
$B_{3,k}(z) \in M_{3^{k}+1}(\Gamma _{0}(144), \chi _2)$
, where
![]() $\chi_2$
is the associated Nebentypus character. Using the same reasoning and (4.3), we find that
$\chi_2$
is the associated Nebentypus character. Using the same reasoning and (4.3), we find that
![]() $\text {PDO}_t(n)$
is divisible by
$\text {PDO}_t(n)$
is divisible by
![]() $3^k$
for almost all
$3^k$
for almost all
![]() $n\geq 0$
. This completes the proof of (1.5).
$n\geq 0$
. This completes the proof of (1.5).
5 Proof of Theorem 1.4
In this section, we prove Theorem 1.4 using nilpotency of Hecke operators. We apply a result of Ono and Taguchi [Reference Ono and Taguchi13] to the modular form
![]() $B_{2,k}(z)$
to deduce the infinite family of congruences.
$B_{2,k}(z)$
to deduce the infinite family of congruences.
Proof of Theorem 1.4
Taking
![]() $p=2$
in (4.3), we have
$p=2$
in (4.3), we have
 $$ \begin{align*} B_{2,k}(z) \equiv \sum_{n=0}^{\infty}\text{PDO}_t(n)q^{n} \pmod {2^{k+1}}. \end{align*} $$
$$ \begin{align*} B_{2,k}(z) \equiv \sum_{n=0}^{\infty}\text{PDO}_t(n)q^{n} \pmod {2^{k+1}}. \end{align*} $$
Note that
![]() $B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
. By [Reference Ono and Taguchi13, Theorem 1.3(3)], there is an integer
$B_{2,k}(z) \in M_{2^{k-1}+1}(\Gamma _{0}(144), \chi _1)$
. By [Reference Ono and Taguchi13, Theorem 1.3(3)], there is an integer
![]() $s\geq 0$
such that for any
$s\geq 0$
such that for any
![]() $u \geq 1$
,
$u \geq 1$
,
whenever
![]() $p_{1}, \ldots , p_{s+u}$
are coprime to
$p_{1}, \ldots , p_{s+u}$
are coprime to
![]() $6$
. It follows from the definition of the Hecke operators that if
$6$
. It follows from the definition of the Hecke operators that if
![]() $p_{1}, \ldots , p_{s+u}$
are distinct primes and if n is coprime to
$p_{1}, \ldots , p_{s+u}$
are distinct primes and if n is coprime to
![]() $p_{1} \cdots p_{s+u}$
, then
$p_{1} \cdots p_{s+u}$
, then
This completes the proof of the theorem.
Acknowledgement
We are very grateful to the referee for the careful reading of the paper and for the comments which helped us to improve the manuscript.