Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T13:08:22.306Z Has data issue: false hasContentIssue false
  • English
  • Français

EIGENVALUE HOMOGENISATION PROBLEM WITH INDEFINITE WEIGHTS

Part of: Spectral theory and eigenvalue problems Partial differential equations

Published online by Cambridge University Press:  15 October 2015

JULIÁN FERNÁNDEZ BONDER ,
JUAN P. PINASCO  and
ARIEL M. SALORT
JULIÁN FERNÁNDEZ BONDER*
Affiliation:
Departamento de Matemática, IMAS – CONICET, FCEyN – Universidad de Buenos Aires, Ciudad Universitaria, Pabellón I, (1428) Av. Cantilo s/n., Buenos Aires, Argentina email jfbonder@dm.uba.ar
JUAN P. PINASCO
Affiliation:
Departamento de Matemática, IMAS – CONICET, FCEyN – Universidad de Buenos Aires, Ciudad Universitaria, Pabellón I, (1428) Av. Cantilo s/n., Buenos Aires, Argentina email jpinasco@dm.uba.ar
ARIEL M. SALORT
Affiliation:
Departamento de Matemática, IMAS – CONICET, FCEyN – Universidad de Buenos Aires, Ciudad Universitaria, Pabellón I, (1428) Av. Cantilo s/n., Buenos Aires, Argentina email asalort@dm.uba.ar
*
✉jfbonder@dm.uba.ar
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this work we study the homogenisation problem for nonlinear elliptic equations involving 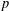$p$-Laplacian-type operators with sign-changing weights. We study the asymptotic behaviour of variational eigenvalues which consist of a double sequence of eigenvalues. We show that the 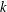$k$th positive eigenvalue goes to infinity when the average of the weights is nonpositive, and converges to the 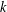$k$th variational eigenvalue of the limit problem when the average is positive for any 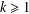$k\geq 1$.

Keywords

p-Laplace-type problemseigenvalueshomogenisationindefinite weights

MSC classification

Primary: 35B27: Homogenization; equations in media with periodic structure
Secondary: 35P15: Estimation of eigenvalues, upper and lower bounds 35P30: Nonlinear eigenvalue problems, nonlinear spectral theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 1 , February 2016 , pp. 113 - 127
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Baffico, L., Conca, C. and Rajesh, M., ‘Homogenization of a class of nonlinear eigenvalue problems’, Proc. Roy. Soc. Edinburgh Sect. A 136(1) (2006), 7–22.CrossRefGoogle Scholar
Braides, A., Chiadò Piat, V. and Defranceschi, A., ‘Homogenization of almost periodic monotone operators’, Ann. Inst. H. Poincaré Anal. Non Linéaire 9(4) (1992), 399–432.CrossRefGoogle Scholar
Champion, T. and De Pascale, L., ‘Asymptotic behaviour of nonlinear eigenvalue problems involving p-Laplacian-type operators’, Proc. Roy. Soc. Edinburgh Sect. A 137(6) (2007), 1179–1195.CrossRefGoogle Scholar
Chiadò Piat, V., Dal Maso, G. and Defranceschi, A., ‘G-convergence of monotone operators’, Ann. Inst. H. Poincaré Anal. Non Linéaire 7(3) (1990), 123–160.CrossRefGoogle Scholar
Fernández Bonder, J., Pinasco, J. P. and Salort, A. M., ‘Eigenvalue homogenization for quasilinear elliptic equations with different boundary conditions’, arXiv:1208.5744 (2012).Google Scholar
Fernández Bonder, J., Pinasco, J. P. and Salort, A. M., ‘A Lyapunov type inequality for indefinite weights and eigenvalue homogenization’, Proc. Amer. Math. Soc., to appear, arXiv:1504.02436 (2015).CrossRefGoogle Scholar
Fernández Bonder, J., Pinasco, J. P. and Salort, A. M., ‘Convergence rate for some quasilinear eigenvalues homogenization problems’, J. Math. Anal. Appl. 423(2) (2015), 1427–1447.CrossRefGoogle Scholar
Fernández Bonder, J., Pinasco, J. P. and Salort, A. M., ‘Some results on quasilinear eigenvalue problems’, Rev. Un. Mat. Argentina 56(1) (2015), 1–25.Google Scholar
Fusco, N. and Moscariello, G., ‘On the homogenization of quasilinear divergence structure operators’, Ann. Mat. Pura Appl. (4) 146 (1987), 1–13.CrossRefGoogle Scholar
Nazarov, S. A., Pankratova, I. L. and Piatnitski, A. L., ‘Homogenization of the spectral problem for periodic elliptic operators with sign-changing density function’, Arch. Ration. Mech. Anal. 200(3) (2011), 747–788.CrossRefGoogle Scholar
Rabinowitz, P. H., Minimax Methods in Critical Point Theory with Applications to Differential Equations, CBMS Regional Conference Series in Mathematics, 65 (Conference Board of the Mathematical Sciences, Washington, DC, 1986).CrossRefGoogle Scholar
Salort, A. M., ‘Eigenvalues homogenization for the fractional laplacian operator’, arXiv:1310.7992 (2013).Google Scholar
Salort, A. M., ‘Convergence rates in a weighted Fuc̆ik problem’, Adv. Nonlinear Stud. 14(2) (2014), 427–443.CrossRefGoogle Scholar