Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T15:02:07.375Z Has data issue: false hasContentIssue false
  • English
  • Français

ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS

Part of: Sequences and sets Finite fields and commutative rings (number-theoretic aspects) Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  16 October 2012

MEI-CHU CHANG
MEI-CHU CHANG*
Affiliation:
Department of Mathematics, University of California, Riverside, USA (email: mcc@math.ucr.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

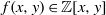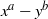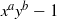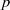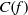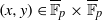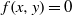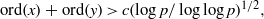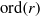Given $f(x,y)\in \mathbb Z[x,y]$ with no common components with $x^a-y^b$ and $x^ay^b-1$, we prove that for $p$ sufficiently large, with $C(f)$ exceptions, the solutions $(x,y)\in \overline {\mathbb F}_p\times \overline {\mathbb F}_p$ of $f(x,y)=0$ satisfy $ {\rm ord}(x)+{\rm ord}(y)\gt c (\log p/\log \log p)^{1/2},$ where $c$ is a constant and ${\rm ord}(r)$ is the order of $r$ in the multiplicative group 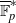$\overline {\mathbb F}_p^*$. Moreover, for most 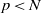$p\lt N$, 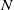$N$ being a large number, we prove that, with 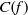$C(f)$ exceptions, 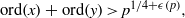${\rm ord}(x)+{\rm ord}(y)\gt p^{1/4+\epsilon (p)},$ where 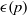$\epsilon (p)$ is an arbitrary function tending to 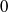$0$ when 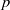$p$ goes to 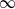$\infty $.

Keywords

multiplicative ordermultiplicative groupfinite fieldsadditive combinatorics

MSC classification

Secondary: 11B75: Other combinatorial number theory 14G15: Finite ground fields 11G20: Curves over finite and local fields 11T06: Polynomials 11T30: Structure theory 11T55: Arithmetic theory of polynomial rings over finite fields 11G99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 169 - 176
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[AR]Ailon, N. & Rudnick, Z., ‘Torsion points on curves and common divisors of $a^k-1$ and $b^k-1$’, Acta Arith. 113 (2004), 31–38.CrossRefGoogle Scholar
[BCZ]Bugeaud, Y., Corvaja, P. & Zannier, U., ‘An upper bound for the G.C.D. of $a^n - 1$ and $b^n- 1$’, Math. Z. 243(1) (2003), 79–84.CrossRefGoogle Scholar
[CJ]Conway, J. H. & Jones, A. J., ‘Trigonometric diophantine equations (on vanishing sums of roots of unity)’, Acta Arith. 30 (1976), 229–240.CrossRefGoogle Scholar
[CZ]Corvaja, P. & Zannier, U., ‘On the maximal order of a torsion point on a curve in $\mathbb G_m^n$’, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Math. Appl. 19(1) (2008), 73–78.CrossRefGoogle Scholar
[CLO]Cox, D. A., Little, J. & O’Shea, D., Ideals, Varieties, and Algorithms (Springer, New York, 1992).CrossRefGoogle Scholar
[DZ]Dvornicich, R. & Zannier, U., ‘On sums of roots of unity’, Monatsh. Math. 129(2) (2000), 97–108.CrossRefGoogle Scholar
[EM]Erdős, P. & Murty, M. R., ‘On the order of $a\,({\rm mod}~ p)$’, Proc. 5th Canadian Number Theory Association Conf. (American Mathematical Society, Providence, RI, 1999), pp. 87–97.CrossRefGoogle Scholar
[E]Evertse, J.-H., ‘The number of solutions of linear equations in roots of unity’, Acta Arith. 89 (1999), 45–51.CrossRefGoogle Scholar
[F]Ford, K., ‘The distribution of integers with a divisor in a given interval’, Ann. of Math. (2) 168 (2008), 367–433.CrossRefGoogle Scholar
[GS]von zur Gathen, J. & Shparlinski, I., ‘Gauss periods in finite fields’, Proc. 5th Conference of Finite Fields and their Applications, Augsburg, 1999 (Springer, Berlin, 2001), pp. 162–177.CrossRefGoogle Scholar
[KPS]Krick, T., Pardo, L. M. & Sombra, M., ‘Sharp estimates for the arithmetic Nullstellensatz’, Duke Math. J. 109(3) (2001), 521–598.CrossRefGoogle Scholar
[L1]Lang, S., ‘Division points on curves’, Annali di Matematica pura ed applicata (IV), Vol. LXX, (1965), 229–234.CrossRefGoogle Scholar
[L2]Lang, S., Fundamentals of Diophantine Geometry (Springer, New York, 1983), pp. 200–207.CrossRefGoogle Scholar
[Sc]Schlickewei, H. P., ‘Equations in roots of unity’, Acta Arith. 76 (1996), 99–108.CrossRefGoogle Scholar
[S1]Shparlinski, I., ‘Additive combinatorics over finite fields: new results and applications’, Proc. RICAM-Workshop on Finite Fields and their Applications: Character Sums and Polynomials (De Gruyter), to appear.Google Scholar
[S2]Shparlinski, I., ‘On the multiplicative orders of $\gamma $ and $\gamma +\gamma ^{-1}$ over finite fields’, Finite Fields Appl. 7 (2001), 327–331.CrossRefGoogle Scholar
[V1]Voloch, J. F., ‘On the order of points on curves over finite fields’, Integers 7 (2007), A49.Google Scholar
[V2]Voloch, J. F., ‘Elements of high order on finite fields from elliptic curves’, Bull. Aust. Math. Soc. 81 (2010), 425–429.CrossRefGoogle Scholar