Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-26T15:25:15.671Z Has data issue: false hasContentIssue false
  • English
  • Français

ELLIPTIC CURVES AND 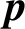$\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE

Part of: Arithmetic algebraic geometry Diophantine approximation, transcendental number theory Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  21 May 2021

DUC HIEP PHAM Open the ORCID record for DUC HIEP PHAM [Opens in a new window]
DUC HIEP PHAM*
Affiliation:
University of Education, Vietnam National University, Hanoi, 144 Xuan Thuy, Cau Giay, Hanoi, Vietnam
*
e-mail: phamduchiep@vnu.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a necessary and sufficient condition for isogenous elliptic curves based on the algebraic dependence of p-adic elliptic functions. As a consequence, we give a short proof of the p-adic analogue of Schneider’s theorem on the linear independence of p-adic elliptic logarithms of algebraic points on two nonisogenous elliptic curves defined over the field of algebraic numbers.

Keywords

elliptic curveelliptic functionp-adic transcendence

MSC classification

Primary: 11J89: Transcendence theory of elliptic and abelian functions
Secondary: 11G07: Elliptic curves over local fields 11S99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 31 - 36
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, A. and Wüstholz, G., Logarithmic Forms and Diophantine Geometry , New Mathematical Monographs, 9 (Cambridge University Press, Cambridge, 2007).Google Scholar
Bertrand, D., ‘Sous-groupes à un paramètre $p$ -adique de variétés de groupe’, Invent. Math. 40(2) (1977), 171–193.CrossRefGoogle Scholar
Bourbaki, N., Elements of Mathematics. Lie groups and Lie algebras. Part I: Chapters 1–3 (Hermann, Paris, 1975).Google Scholar
Fuchs, C. and Pham, D. H., ‘The $p$ -adic analytic subgroup theorem revisited’, $p$ -Adic Numbers Ultrametric Anal. Appl. 7 (2015), 143–156.CrossRefGoogle Scholar
Fuchs, C. and Pham, D. H., ‘Some applications of the $p$ -adic analytic subgroup theorem’, Glas. Mat. 51 (2016), 335–343.CrossRefGoogle Scholar
Lutz, E., ‘Sur l’équation ${Y}^2=A{X}^3-\mathrm{AX}-B$ dans les corps $p$ -adiques’, J. reine angew. Math. 177 (1937), 238–247.CrossRefGoogle Scholar
Murty, M. R. and Rath, P., Transcendental Numbers (Springer, New York, 2014).Google Scholar
Schneider, T., ‘Arithmetische Untersuchungen elliptischer Integrale’, Math. Ann. 113 (1936), 1–13.CrossRefGoogle Scholar
Schneider, T., Einführung in die Transzendenten Zahlen (Springer-Verlag, Berlin, 1957).CrossRefGoogle Scholar
Weil, A., ‘Sur les fonctions elliptiques $p$ -adiques’, Note aux C. R. Acad. Sci. Paris 203 (1936), 22–24.Google Scholar
Wüstholz, G., ‘Algebraische Punkte auf analytischen Untergruppen algebraischer Gruppen’, Ann. of Math. 129 (1989), 501–517.CrossRefGoogle Scholar
Zarhin, Y. G., ‘ $p$ -adic abelian integrals and commutative Lie groups’, J. Math. Sci. 81(3) (1996), 2744–2750.CrossRefGoogle Scholar