EMBEDDING OF METRIC GRAPHS ON HYPERBOLIC SURFACES

Abstract

An embedding of a metric graph 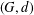$(G,d)$ on a closed hyperbolic surface is essential if each complementary region has a negative Euler characteristic. We show, by construction, that given any metric graph, its metric can be rescaled so that it admits an essential and isometric embedding on a closed hyperbolic surface. The essential genus 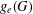$g_{e}(G)$ of 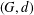$(G,d)$ is the lowest genus of a surface on which such an embedding is possible. We establish a formula to compute 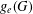$g_{e}(G)$ and show that, for every integer 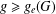$g\geq g_{e}(G)$, there is an embedding of 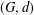$(G,d)$ (possibly after a rescaling of 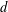$d$) on a surface of genus 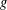$g$. Next, we study minimal embeddings where each complementary region has Euler characteristic 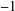$-1$. The maximum essential genus 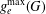$g_{e}^{\max }(G)$ of 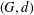$(G,d)$ is the largest genus of a surface on which the graph is minimally embedded. We describe a method for an essential embedding of 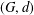$(G,d)$, where 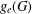$g_{e}(G)$ and 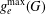$g_{e}^{\max }(G)$ are realised.