ENTIRE SOLUTIONS OF A CURVATURE FLOW IN AN UNDULATING CYLINDER

Abstract

We consider a curvature flow 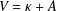$V=\unicode[STIX]{x1D705}+A$ in a two-dimensional undulating cylinder 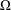$\unicode[STIX]{x1D6FA}$ described by 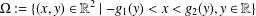$\unicode[STIX]{x1D6FA}:=\{(x,y)\in \mathbb{R}^{2}\mid -g_{1}(y)<x<g_{2}(y),y\in \mathbb{R}\}$, where 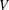$V$ is the normal velocity of a moving curve contacting the boundaries of 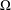$\unicode[STIX]{x1D6FA}$ perpendicularly, $\unicode[STIX]{x1D705}$ is its curvature, 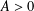$A>0$ is a constant and 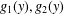$g_{1}(y),g_{2}(y)$ are positive smooth functions. If 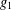$g_{1}$ and 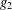$g_{2}$ are periodic functions and there are no stationary curves, Matano et al. [‘Periodic traveling waves in a two-dimensional cylinder with saw-toothed boundary and their homogenization limit’, Netw. Heterog. Media1 (2006), 537–568] proved the existence of a periodic travelling wave. We consider the case where 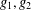$g_{1},g_{2}$ are general nonperiodic positive functions and the problem has some stationary curves. For each stationary curve 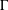$\unicode[STIX]{x1D6E4}$ unstable from above/below, we construct an entire solution growing out of it, that is, a solution curve 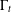$\unicode[STIX]{x1D6E4}_{t}$ which increases/decreases monotonically, converging to 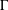$\unicode[STIX]{x1D6E4}$ as 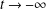$t\rightarrow -\infty$ and converging to another stationary curve or to 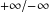$+\infty /-\infty$ as 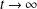$t\rightarrow \infty$.