Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T03:36:39.304Z Has data issue: false hasContentIssue false
  • English
  • Français

EXTREME VALUES OF THE RANKIN–SELBERG 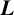$\boldsymbol {L}$-FUNCTIONS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  21 March 2022

CHI CUI Open the ORCID record for CHI CUI [Opens in a new window]  and
QIYU YANG Open the ORCID record for QIYU YANG [Opens in a new window]
CHI CUI
Affiliation:
Faculty of Information Technology, Macau University of Science and Technology, Macau, PR China e-mail: ccuicynthia@gmail.com
QIYU YANG*
Affiliation:
Faculty of Information Technology, Macau University of Science and Technology, Macau, PR China
*
e-mail: qyyang.must@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the extreme values of the Rankin–Selberg L-functions associated with holomorphic cusp forms in the vertical direction. Assuming the generalised Riemann hypothesis (GRH), we prove that

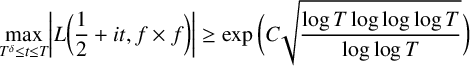$$ \begin{align*} \underset{T^{\delta}\leq t\leq T}{\max}\bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert \geq\exp\bigg(C\sqrt{\frac{\log T\log\log\log T}{\log\log T}}\bigg) \end{align*} $$

with 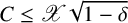$C\leq \mathscr {X}\sqrt {1-\delta }$ , where 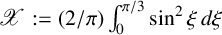$\mathscr {X}:=({2}/{\pi })\int _{0}^{\pi /3}\sin ^2\xi \,d\xi $ and 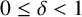$0\leq \delta <1$ .

Keywords

extreme valueresonance methodRankin–Selberg L-function

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight
Secondary: 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 408 - 418
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Science and Technology Development Fund, Macau SAR (File No. 0066/2020/A2).

References

Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., ‘A family of Calabi–Yau varieties and potential automorphy II’, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98.CrossRefGoogle Scholar
Bondarenko, A. and Seip, K., ‘Large greatest common divisor sums and extreme values of the Riemann zeta function’, Duke Math. J. 166 (2017), 1685–1701.CrossRefGoogle Scholar
Bondarenko, A. and Seip, K., ‘Extreme values of the Riemann zeta function and its argument’, Math. Ann. 372 (2018), 999–1015.CrossRefGoogle Scholar
Chandee, V. and Soundararajan, K., ‘Bounding $|\zeta(\frac{1}{2}+it)|$ on the Riemann hypothesis’, Bull. Lond. Math. Soc. 43 (2011), 243–250.10.1112/blms/bdq095CrossRefGoogle Scholar
De la Bretèche, R. and Tenenbaum, G., ‘Sommes de Gál et applications’, Proc. Lond. Math. Soc. 119 (2019), 104–134.CrossRefGoogle Scholar
Deligne, P., ‘La Conjecture de Weil I’, Publ. Math. lnst. Hautes Études Sci. 43 (1974), 273–307.CrossRefGoogle Scholar
Hilberdink, T., ‘An arithmetical mapping and applications to Ω-results for theRiemann zeta function’, Acta Arith. 139 (2009), 341–367.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Littlewood, J. E., ‘On the zeros of the Riemann zeta-function’, Math. Proc. Cambridge Philos. Soc. 22 (1924), 295–318.CrossRefGoogle Scholar
Soundararajan, K., ‘Extreme values of zeta and $L$ -functions’, Math. Ann. 342 (2008), 467–486.CrossRefGoogle Scholar
Tang, H. and Xiao, X., ‘Integral moments of automorphic $L$ -functions’, Int. J. Number Theory 12 (2016), 1827–1843.CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (Oxford University Press, New York, 1986), edited and with a preface by D. R. Heath-Brown.Google Scholar
Voronin, S. M., ‘Lower bounds in Riemann zeta-function theory’, Izv. Akad. Nauk SSSR Ser. Mat. 52 (1988), 882–892.Google Scholar