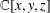Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sun, Xiaosong
and
Liu, Dayan
2021.
Images of locally nilpotent derivations of polynomial algebras in three variables.
Journal of Algebra,
Vol. 569,
Issue. ,
p.
401.
Tian, Haifeng
Du, Xiankun
and
Jia, Hongyu
2022.
Images of linear derivations and linear E-derivations of K[x,y,z].
Communications in Algebra,
Vol. 50,
Issue. 7,
p.
3124.
SUN, XIAOSONG
and
WANG, BEINI
2023.
ON THE LND CONJECTURE.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 3,
p.
412.
Jia, Hongyu
Du, Xiankun
and
Tian, Haifeng
2023.
Images of locally finite E-derivations of bivariate polynomial algebras.
Journal of Algebra,
Vol. 630,
Issue. ,
p.
162.
Gupta, Sakshi
Ahuja, Divya
and
Kour, Surjeet
2023.
Image of linear
K
-derivations and linear ΚƐ-derivations of
K
[
x
1
,
x
2
,
x
3
,
x
4
]
.
Communications in Algebra,
Vol. 51,
Issue. 12,
p.
5091.
Gupta, Sakshi
2025.
Image of ideals under linear K-derivations and the LNED conjecture.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 9,
p.
108041.