Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cossey, John
1987.
Finite soluble groups have large centralisers.
Bulletin of the Australian Mathematical Society,
Vol. 35,
Issue. 2,
p.
291.

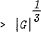 if, for example, |
if, for example, |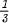 can be improved to
can be improved to 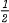 , for example when
, for example when 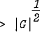 whenever
whenever 