No CrossRef data available.
Article contents
FINITELY STABLE ADDITIVE BASES
Published online by Cambridge University Press: 20 February 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
An additive basis 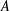 $A$ is finitely stable when the order of
$A$ is finitely stable when the order of 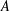 $A$ is equal to the order of
$A$ is equal to the order of 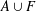 $A\cup F$ for all finite subsets
$A\cup F$ for all finite subsets 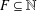 $F\subseteq \mathbb{N}$ . We give a sufficient condition for an additive basis to be finitely stable. In particular, we prove that
$F\subseteq \mathbb{N}$ . We give a sufficient condition for an additive basis to be finitely stable. In particular, we prove that 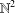 $\mathbb{N}^{2}$ is finitely stable.
$\mathbb{N}^{2}$ is finitely stable.
MSC classification
Secondary:
11P05: Waring's problem and variants
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
Landau, E., ‘Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindestzahl der zu ihrer additiven Zusammensetzung erforderlichen Quadrate’, Arch. Math. Phys.
13(3) (1908), 305–312.Google Scholar
Nathanson, M. B., Additive Number Theory: The Classical Bases, Graduate Texts in Mathematics, 164 (Springer, New York, 1996).CrossRefGoogle Scholar

