Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hayashi, Nakao
and
Naumkin, Pavel I.
2015.
Large time asymptotics for the fourth-order nonlinear Schrödinger equation.
Journal of Differential Equations,
Vol. 258,
Issue. 3,
p.
880.
Hayashi, Nakao
and
Naumkin, Pavel I.
2015.
Global existence and asymptotic behavior of solutions to the fourth-order nonlinear Schrödinger equation in the critical case.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 116,
Issue. ,
p.
112.
Hayashi, Nakao
and
Naumkin, Pavel I.
2015.
Factorization technique for the fourth-order nonlinear Schrödinger equation.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 5,
p.
2343.
Hirayama, Hiroyuki
and
Okamoto, Mamoru
2016.
Well-posedness and scattering for fourth order nonlinear Schrödinger type equations at the scaling critical regularity.
Communications on Pure and Applied Analysis,
Vol. 15,
Issue. 3,
p.
831.
Aoki, Kazuki
Hayashi, Nakao
and
Naumkin, Pavel I.
2016.
Global existence of small solutions for the fourth-order nonlinear Schrödinger equation .
Nonlinear Differential Equations and Applications NoDEA,
Vol. 23,
Issue. 6,
Hayashi, Nakao
Mendez-Navarro, Jesus A.
and
Naumkin, Pavel I.
2016.
Asymptotics for the fourth-order nonlinear Schrödinger equation in the critical case.
Journal of Differential Equations,
Vol. 261,
Issue. 9,
p.
5144.
Hayashi, Nakao
Mendez-Navarro, Jesus A.
and
Naumkin, Pavel I.
2016.
Scattering of solutions to the fourth-order nonlinear Schrödinger equation.
Communications in Contemporary Mathematics,
Vol. 18,
Issue. 03,
p.
1550035.
Liu, Changchun
Wang, Huimin
and
Feng, Zhaosheng
2020.
Global solution for a sixth-order nonlinear Schrödinger equation.
Journal of Mathematical Analysis and Applications,
Vol. 490,
Issue. 2,
p.
124327.
Hirayama, Hiroyuki
Ikeda, Masahiro
and
Tanaka, Tomoyuki
2021.
Well-posedness for the fourth-order Schrödinger equation with third order derivative nonlinearities.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 28,
Issue. 5,
Aoki, Kazuki
2021.
Global existence of small solutions for a quadratic nonlinear fourth-order Schrödinger equation in six space dimensions.
Tohoku Mathematical Journal,
Vol. 73,
Issue. 1,
Lu, Yufeng
2023.
Well‐posedness of generalized KdV and one‐dimensional fourth‐order derivative nonlinear Schrödinger equations for data with an infinite L2 norm.
Studies in Applied Mathematics,
Vol. 150,
Issue. 3,
p.
883.


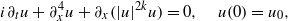
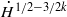 . With small initial data we obtain global well-posedness results. Our proof relies heavily on the method developed by Kenig
. With small initial data we obtain global well-posedness results. Our proof relies heavily on the method developed by Kenig 