Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T06:24:32.273Z Has data issue: false hasContentIssue false
  • English
  • Français

GRAPHS DETERMINED BY THEIR 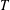$T$-GAIN SPECTRA

Part of: Graph theory

Published online by Cambridge University Press:  03 July 2020

SAI WANG Open the ORCID record for SAI WANG [Opens in a new window] ,
DEIN WONG  and
FENGLEI TIAN
SAI WANG*
Affiliation:
School of Mathematics,China University of Mining and Technology, Xuzhou221116, Jiangsu, PR China email 27624181@qq.com Xuhai College, China University of Mining and Technology, Jiangsu, PR China
DEIN WONG
Affiliation:
School of Mathematics,China University of Mining and Technology, Xuzhou, PR China email wongdein@163.com
FENGLEI TIAN
Affiliation:
School of Management,Qufu Normal University, Rizhao, 276826, Shandong, PR China email tflqsd@126.com
*
✉27624181@qq.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An undirected graph 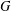$G$ is determined by its 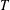$T$-gain spectrum (DTS) if every 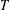$T$-gain graph cospectral to 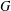$G$ is switching equivalent to 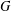$G$. We show that the complete graph 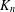$K_{n}$ and the graph $K_{n}-e$ obtained by deleting an edge from 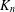$K_{n}$ are DTS, the star 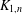$K_{1,n}$ is DTS if and only if 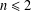$n\leq 2$, and an odd path 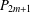$P_{2m+1}$ is not DTS if 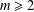$m\geq 2$. We give an operation for constructing cospectral 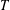$T$-gain graphs and apply it to show that a tree of arbitrary order (at least $5$) is not DTS.

Keywords

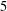complex unit gain graphsgraphs determined by their spectracospectral graphs

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 05C22: Signed and weighted graphs
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 195 - 203
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the National Natural Science Foundation of China (No.11971474). The third author is supported by the Natural Science Foundation of Shandong Province (No. ZR2019BA016).

References

Collatz, L. and Sinogowitz, U., ‘Spektren endlicher Grafen’, Abh. Math. Semin. Univ. Hambg. 21 (1957), 63–77.Google Scholar
van Dam, E. R. and Haemers, W. H., ‘Which graphs are determined by their spectrum?’, Special Issue on the Combinatorial Matrix Theory Conference, Pohang, 2002’, Linear Algebra Appl. 373 (2003), 241–272.Google Scholar
van Dam, E. R. and Haemers, W. H., ‘Developments on spectral characterizations of graphs’, Discrete Math. 309 (2009), 576–586.Google Scholar
Godsil, C. D. and McKay, B. D., ‘Constructing cospectral graphs’, Aequationes Math. 25 (1982), 257–268.Google Scholar
Günthard, H. H. and Primas, H., ‘Zusammenhang von Graphentheorie und MO-Theorie von Molekelnmit Systemen konjugierter Bindungen’, Helv. Chim. Acta 39 (1956), 1645–1653.Google Scholar
Kac, M., ‘Can one hear the shape of a drum?’, Amer. Math. Monthly 73 (1966), 162–179.Google Scholar
Lu, Y., Wang, L. G. and Xiao, P., ‘Complex unit gain bicyclic graphs with rank 2, 3 or 4’, Linear Algebra Appl. 523 (2017), 169–186.Google Scholar
Lu, Y., Wang, L. G. and Zhou, Q., ‘The rank of a complex unit gain graph in terms of the rank of its underlying graph’, J. Comb. Optim. 38 (2019), 570–588.Google Scholar
McKay, B. D., ‘On the spectral characterisation of trees’, Ars Combin. 3 (1977), 219–232.Google Scholar
Reff, N., ‘Spectral properties of complex unit gain graphs’, Linear Algebra Appl. 436 (2012), 3165–3176.Google Scholar
Schwenk, A. J., ‘Almost all trees are cospectral’, in: New Directions in the Theory of Graphs, Proceedings of the 3rd Ann Arbor Conference, University of Michigan, Ann Arbor, Michigan, 1971 (Academic Press, New York, 1973), 275–307.Google Scholar
Wang, Y., Gong, S. C. and Fan, Y. Z., ‘On the determinant of the Laplacian matrix of a complex unit gain graph’, Discrete Math. 341 (2018), 81–86.Google Scholar
Yu, G. H., Qu, H. and Tu, J. H., ‘Inertia of complex unit gain graphs’, Appl. Math. Comput. 265 (2015), 619–629.Google Scholar
Zaslavsky, T., ‘Biased graphs. I. Bias, balance and gains’, J. Combin. Theory Ser. B 47 (1989), 32–52.Google Scholar