Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T17:15:30.770Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WHOSE PROPER SUBGROUPS OF INFINITE RANK HAVE FINITE CONJUGACY CLASSES

Published online by Cambridge University Press:  11 February 2013

M. DE FALCO ,
F. DE GIOVANNI ,
C. MUSELLA  and
N. TRABELSI
M. DE FALCO
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, I - 80126 Napoli, Italy email mdefalco@unina.itcmusella@unina.it
F. DE GIOVANNI*
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, I - 80126 Napoli, Italy email mdefalco@unina.itcmusella@unina.it
C. MUSELLA
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, I - 80126 Napoli, Italy email mdefalco@unina.itcmusella@unina.it
N. TRABELSI
Affiliation:
Laboratory of Fundamental and Numerical Mathematics, Department of Mathematics, University of Setif, Setif 19000, Algeria email nadir_trabelsi@yahoo.fr
*
✉degiovan@unina.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

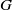A group $G$ is said to be an 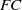$FC$-group if each element of 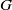$G$ has only finitely many conjugates, and 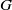$G$ is minimal non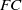$FC$ if all its proper subgroups have the property 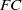$FC$ but 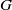$G$ is not an 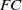$FC$-group. It is an open question whether there exists a group of infinite rank which is minimal non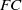$FC$. We consider here groups of infinite rank in which all proper subgroups of infinite rank are 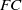$FC$, and prove that in most cases such groups are either 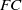$FC$-groups or minimal non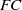$FC$.

Keywords

finite rankFC-group
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 41 - 48
Copyright
©2013 Australian Mathematical Publishing Association Inc. 

References

Amberg, B., Franciosi, S. and de Giovanni, F., Products of Groups (Clarendon Press, Oxford, 1992).Google Scholar
Belyaev, V. V., ‘Minimal non-FC-groups’, Proc. All Union Symposium on Group Theory (Kiev, 1980), pp. 97–108.Google Scholar
Belyaev, V. V. and Sesekin, N. F., ‘On infinite groups of Miller–Moreno type’, Acta Math. Acad. Sci. Hungar. 26 (1975), 369–376.Google Scholar
Černikov, N. S., ‘A theorem on groups of finite special rank’, Ukrainian Math. J. 42 (1990), 855–861.Google Scholar
De Falco, M., de Giovanni, F., Musella, C. and Trabelsi, N., ‘Groups with restrictions on subgroups of infinite rank’, Rev. Mat. Iberoamericana, to appear.Google Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Locally soluble-by-finite groups of finite rank’, J. Algebra 182 (1996), 756–769.CrossRefGoogle Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Locally (soluble-by-finite) groups with all proper nonnilpotent subgroups of finite rank’, J. Pure Appl. Algebra 135 (1999), 33–43.Google Scholar
Dixon, M. R., Evans, M. J. and Smith, H., ‘Groups with all proper subgroups (finite rank)-by-nilpotent’, Arch. Math. (Basel) 72 (1999), 321–327.CrossRefGoogle Scholar
Franciosi, S., de Giovanni, F. and Sysak, Y. P., ‘Groups with many FC-subgroups’, J. Algebra 218 (1999), 165–182.Google Scholar
Kleidman, P. B. and Wilson, R. A., ‘A characterization of some locally finite simple groups of Lie type’, Arch. Math. (Basel) 48 (1987), 10–14.Google Scholar
Kuzucuoglu, M. and Phillips, R. E., ‘Locally finite minimal non-FC-groups’, Math. Proc. Cambridge Philos. Soc. 105 (1989), 417–420.Google Scholar
Otal, J. and Peña, J. M., ‘Infinite locally finite groups of type PSL(2,K) or Sz(K) are not minimal under certain conditions’, Publ. Mat. 32 (1988), 43–47.Google Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).Google Scholar
Šunkov, V. P., ‘On locally finite groups of finite rank’, Algebra Logic 10 (1971), 127–142.CrossRefGoogle Scholar
Tomkinson, M. J., FC-groups (Pitman, Boston, 1984).Google Scholar