Hostname: page-component-784d4fb959-8cb88 Total loading time: 0 Render date: 2025-07-16T13:08:39.975Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WITH DENSE TRANSITIVELY NORMAL SUBGROUPS

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  07 July 2025

ALESSIO RUSSO Open the ORCID record for ALESSIO RUSSO [Opens in a new window]
ALESSIO RUSSO*
Affiliation:
Dipartimento di Matematica e Fisica, https://ror.org/02kqnpp86 Università della Campania ‘Luigi Vanvitelli’, Caserta, Italy
*
e-mail: alessio.russo@unicampania.it
Get access Rights & Permissions [Opens in a new window]

Abstract

A subgroup X of a group G is said to be transitively normal if X is normal in any subgroup Y of G such that 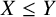$X\leq Y$ and X is subnormal in Y. We investigate the structure of generalised soluble groups with dense transitively normal subgroups, that is, groups in which every nonempty open interval in their subgroup lattice contains a transitively normal subgroup. In particular, it will be proved that nonperiodic generalised soluble groups with dense transitively normal subgroups are abelian.

Keywords

transitively normal subgroupT-groupdensitygeneralised soluble group

MSC classification

Primary: 20F19: Generalizations of solvable and nilpotent groups
Secondary: 20E15: Chains and lattices of subgroups, subnormal subgroups 20F16: Solvable groups, supersolvable groups

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is a member of GNSAGA-INdAM and ADV-AGTA.

References

de Giovanni, F. and Russo, A., ‘Groups with dense subnormal subgroups’, Rend. Sem. Mat. Univ. Padova 101 (1999), 19–27.Google Scholar
de Giovanni, F., Russo, A. and Vincenzi, G., ‘Groups in which every subgroup is almost pronormal’, Note Mat. 1 (2008), 95–103.Google Scholar
Gaschütz, W., ‘Gruppen, in denen das Normalteilersein transitiv ist’, J. reine angew. Math. 198 (1957), 87–92.10.1515/crll.1957.198.87CrossRefGoogle Scholar
Khukhro, E. I. and Mazurov, V. D., Kourova Notebook, Vol. 16 (Russian Academy of Sciences, Novosibirsk, 2006).Google Scholar
Kurdachenko, L. A., Kuzennyi, N. F. and Semko, N. N., ‘Groups with a dense system of infinite almost normal subgroups’, Ukrainian Math. J. 43 (1991), 904–908.10.1007/BF01058691CrossRefGoogle Scholar
Kurdachenko, L. A. and Subbotin, I. Y., ‘Transitivity of normality and pronormal subgroups’, Contemp. Math. 421 (2006), 201–212.10.1090/conm/421/08038CrossRefGoogle Scholar
Longobardi, P., Maj, M. and Smith, H., ‘A note on locally graded groups’, Rend. Sem. Mat. Univ. Padova 94 (1995), 275–277.Google Scholar
Mahdavianary, S. K., ‘A special class of three-Engel groups’, Arch. Math. (Basel) 40 (1983), 193–199.10.1007/BF01192771CrossRefGoogle Scholar
Mann, A., ‘Groups with dense normal subgroups’, Israel J. Math. 6 (1968), 13–25.10.1007/BF02771600CrossRefGoogle Scholar
Müller, K. H., ‘Schwachnormale Untergruppen: Eine gemeinsame Verallgemeinerung der normalen und normalisatorgleichen Untergruppen’, Rend. Sem. Mat. Univ. Padova 36 (1966), 129–157.Google Scholar
Robinson, D. J. S., ‘Groups in which normality is a transitive relation’, Proc. Cambridge Philos. Soc. 60 (1964), 21–38.10.1017/S0305004100037403CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer-Verlag, New York, 1995).Google Scholar
Robinson, D. J. S., Russo, A. and Vincenzi, G., ‘On groups which contain no HNN-extension’, Internat. J. Algebra Comput. 17 (2005), 1377–1387.10.1142/S0218196707004311CrossRefGoogle Scholar
Russo, A., ‘On groups in which normality is a transitive relation’, Comm. Algebra 40 (2012), 3950–3954.10.1080/00927872.2011.610076CrossRefGoogle Scholar
Vincenzi, G., ‘Groups with dense pronormal subgroups’, Ricerche Mat. 40 (1991), 75–79.Google Scholar