Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T17:40:22.403Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS WITH THE SAME CHARACTER DEGREES AS SPORADIC ALMOST SIMPLE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  23 May 2016

SEYED HASSAN ALAVI ,
ASHRAF DANESHKHAH  and
ALI JAFARI
SEYED HASSAN ALAVI
Affiliation:
Department of Mathematics, Faculty of Science, Bu-Ali Sina University, Hamedan, Iran email alavi.s.hassan@gmail.com
ASHRAF DANESHKHAH*
Affiliation:
Department of Mathematics, Faculty of Science, Bu-Ali Sina University, Hamedan, Iran email daneshkhah.ashraf@gmail.com, adanesh@basu.ac.ir
ALI JAFARI
Affiliation:
Department of Mathematics, Faculty of Science, Bu-Ali Sina University, Hamedan, Iran email a.jaefary@gmail.com
*
✉daneshkhah.ashraf@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 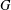$G$ be a finite group and 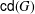$\mathsf{cd}(G)$ denote the set of complex irreducible character degrees of 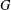$G$. We prove that if 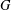$G$ is a finite group and 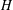$H$ is an almost simple group whose socle is a sporadic simple group 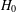$H_{0}$ and such that 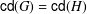$\mathsf{cd}(G)=\mathsf{cd}(H)$, then 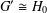$G^{\prime }\cong H_{0}$ and there exists an abelian subgroup 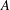$A$ of 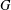$G$ such that 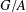$G/A$ is isomorphic to 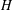$H$. In view of Huppert’s conjecture, we also provide some examples to show that 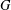$G$ is not necessarily a direct product of 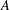$A$ and 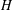$H$, so that we cannot extend the conjecture to almost simple groups.

Keywords

character degreesalmost simple groupssporadic simple groupsHuppert’s conjecture

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D05: Finite simple groups and their classification
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 254 - 265
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alavi, S. H., Daneshkah, A., Tong-Viet, H. P. and Wakefield, T. P., ‘Huppert’s conjecture for Fi 23 ’, Rend. Semin. Mat. Univ. Padova 126 (2011), 201–211.Google Scholar
Alavi, S. H., Daneshkhah, A. and Jafari, A., ‘On groups with the same character degrees as almost simple groups with socle the Mathieu groups’, preprint arXiv:1511.04129, November, 2015.Google Scholar
Alavi, S. H., Daneshkhah, A., Tong-Viet, H. P. and Wakefield, T. P., ‘On Huppert’s conjecture for the Conway and Fischer families of sporadic simple groups’, J. Aust. Math. Soc. 94(3) (2013), 289–303.Google Scholar
Bianchi, M., Chillag, D., Lewis, M. L. and Pacifici, E., ‘Character degree graphs that are complete graphs’, Proc. Amer. Math. Soc. 135(3) (2007), 671–676; (electronic).CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A., Wilson, R. A. and (with computational assistance from J. G. Thackray), Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups (Oxford University Press, Eynsham, 1985).Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.8.2, (2016). http://www.gap-system.org/Releases/.Google Scholar
Huppert, B., Character Theory of Finite Groups, de Gruyter Expositions in Mathematics, 25 (Walter de Gruyter & Co., Berlin, 1998).Google Scholar
Huppert, B., ‘Some simple groups which are determined by the set of their character degrees. I’, Illinois J. Math. 44(4) (2000), 828–842.Google Scholar
Huppert, B., ‘Some simple groups which are determined by the set of their character degrees III–VIII,’ Technical Report, Institut für Experimentelle Mathematik, Universtät, Essen, 2000.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (AMS Chelsea Publishing, Providence, RI, 2006).Google Scholar
Moretó, A., ‘An answer to a question of Isaacs on character degree graphs’, Adv. Math. 201(1) (2006), 90–101.Google Scholar
Tong-Viet, H. P. and Wakefield, T. P., ‘On Huppert’s conjecture for the Monster and Baby Monster’, Monatsh. Math. 167(3–4) (2012), 589–600.Google Scholar