Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bao, Guanlong
Ye, Fangqin
and
Zhu, Kehe
2021.
Hankel Measures for Hardy Spaces.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 5,
p.
5131.
Xiao, Jie
and
Yuan, Cheng
2022.
Cauchy-Riemann ̄∂-equations with some applications.
Complex Manifolds,
Vol. 9,
Issue. 1,
p.
170.
Liu, Yongqing
and
Hou, Shengzhao
2022.
Pseudo-Carleson Measures for Fock Spaces.
Taiwanese Journal of Mathematics,
Vol. 26,
Issue. 6,
Biqian, Wu
and
Guangfu, Cao
2023.
The pseudo-Carleson measure for the Fock-Sobolev space.
SCIENTIA SINICA Mathematica,
Vol. 53,
Issue. 12,
p.
1827.
Sun, Fangmei
and
Ye, Fangqin
2023.
Characterizations of Hankel type measures.
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 1,
p.
127434.
WANG, ERMIN
2023.
HANKEL MEASURES FOR FOCK SPACE.
Bulletin of the Australian Mathematical Society,
Vol. 107,
Issue. 2,
p.
290.
Zhou, Zhihui
2024.
Hankel-Type Operator Acting on Hardy Spaces and Weighted Bergman Spaces.
Complex Analysis and Operator Theory,
Vol. 18,
Issue. 4,
Zorboska, Nina
2024.
Measure induced Hankel and Toeplitz type operators on weighted Dirichlet spaces.
Proceedings of the American Mathematical Society, Series B,
Vol. 11,
Issue. 9,
p.
84.


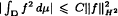 for all
for all 