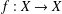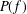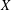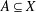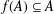Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lazaar, Sami
Richmond, Tom
and
Sabri, Houssem
2019.
The autohomeomorphism group of connected homogeneous functionally Alexandroff spaces.
Communications in Algebra,
Vol. 47,
Issue. 9,
p.
3818.
Chiaselotti, Giampiero
and
Infusino, Federico G.
2020.
Alexandroff topologies and monoid actions.
Forum Mathematicum,
Vol. 32,
Issue. 3,
p.
795.
García-Ferreira, S.
Guale, A.
and
Vielma, J.
2021.
Primal topologies on the integers.
Quaestiones Mathematicae,
Vol. 44,
Issue. 4,
p.
435.
Menix, Jacob
and
Richmond, Tom
2021.
The Lattice of Functional Alexandroff Topologies.
Order,
Vol. 38,
Issue. 1,
p.
1.
Amor, Ahlem Ben
Lazaar, Sami
Richmond, Tom
and
Sabri, Houssem
2022.
k-primal spaces.
Topology and its Applications,
Vol. 309,
Issue. ,
p.
107907.
Echi, Othman
2022.
ON A TOPOLOGY DEFINED BY PRIMITIVE WORDS.
Missouri Journal of Mathematical Sciences,
Vol. 34,
Issue. 2,
Echi, Othman
2022.
On the product of primal spaces.
Quaestiones Mathematicae,
Vol. 45,
Issue. 1,
p.
1.
Mhemdi, Abdelwaheb
Lazaar, Sami
Dourari, Khedidja
and
Khalil, Ahmed Mostafa
2022.
On Some Properties of Whyburn Spaces.
Computational Intelligence and Neuroscience,
Vol. 2022,
Issue. ,
p.
1.
Lazaar, Sami
Sabri, Houssem
and
Tahri, Randa
2022.
Structural and Numerical Studies of Some Topological Properties for Alexandroff Spaces.
Bulletin of the Iranian Mathematical Society,
Vol. 48,
Issue. 4,
p.
1575.
Sabri, Houssem
2022.
An enumeration of distinct and non-isomorphic functional quasi-order relations.
Discrete Mathematics,
Vol. 345,
Issue. 11,
p.
113039.
Alshehri, Maryam
Lazaar, Sami
Mhemdi, Abdelwaheb
and
Zidani, Neama
2023.
Some separation axioms for partially ordered sets.
Filomat,
Vol. 37,
Issue. 7,
p.
2173.
Infusino, F.
2023.
On a quotient S-set induced by countably infinite decreasing chains.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 69,
Issue. 2,
p.
561.