Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T20:08:32.252Z Has data issue: false hasContentIssue false
  • English
  • Français

HYPERGROUP ALGEBRAS AS TOPOLOGICAL ALGEBRAS

Part of: Topological linear spaces and related structures Abstract harmonic analysis Topological algebras, normed rings and algebras, Banach algebras

Published online by Cambridge University Press:  13 June 2014

S. MAGHSOUDI  and
J. B. SEOANE-SEPÚLVEDA
S. MAGHSOUDI
Affiliation:
Department of Mathematics, University of Zanjan, Zanjan 45195-313, Iran email s_maghsodi@znu.ac.ir
J. B. SEOANE-SEPÚLVEDA*
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias Matemáticas, Universidad Complutense de Madrid, Plaza de Ciencias 3, Madrid 28040, Spain email jseoane@mat.ucm.es
*
✉jseoane@mat.ucm.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 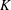$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$ be a locally compact hypergroup endowed with a left Haar measure and let 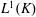$L^1(K)$ be the usual Lebesgue space of 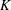$K$ with respect to the left Haar measure. We investigate some properties of 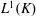$L^1(K)$ under a locally convex topology 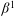$\beta ^1$. Among other things, the semireflexivity of 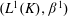$(L^1(K), \beta ^1)$ and of sequentially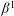$\beta ^1$-continuous functionals is studied. We also show that 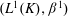$(L^1(K), \beta ^1)$ with the convolution multiplication is always a complete semitopological algebra, whereas it is a topological algebra if and only if 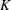$K$ is compact.

Keywords

locally compact hypergroupstrict topologyhypergroup algebratopological algebra

MSC classification

Secondary: 43A62: Hypergroups 46A70: Saks spaces and their duals (strict topologies, mixed topologies, two-norm spaces, co-Saks spaces, etc.) 43A20: $L^1$-algebras on groups, semigroups, etc. 46H05: General theory of topological algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 486 - 493
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bloom, W. R. and Heyer, H., Harmonic Analysis of Probability Measures on Hypergroups, De Gruyter Studies in Mathematics, 20 (Walter de Gruyter, Berlin, 1995).CrossRefGoogle Scholar
Dunkl, C. F., ‘The measure algebra of a locally compact hypergroup’, Trans. Amer. Math. Soc. 179 (1973), 331–348.Google Scholar
Ghaffari, A., ‘Convolution operators on the dual of hypergroup algebras’, Comment. Math. Univ. Carolin. 44 (2003), 669–679.Google Scholar
Grosser, M., Bidualräume und Vervollständigungen von Banachmoduln, Lecture Notes in Mathematics, 717 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Hewitt, E. and Stromberg, K., Real and Abstract Analysis (Springer, New York, 1975).Google Scholar
Jewett, R. I., ‘Spaces with an abstract convolution of measures’, Adv. Math. 18 (1975), 1–101.Google Scholar
Khan, L. A., ‘Topological modules of continuous homomorphisms’, J. Math. Anal. Appl. 343 (2008), 141–150.Google Scholar
Khan, L. A., ‘The general strict topology on topological modules’, in: Function Spaces, Contemporary Mathematics, 435 (American Mathematical Society, Providence, RI, 2007), 253–263.Google Scholar
Khan, L. A., Mohammad, N. and Thaheem, A. B., ‘The strict topology on topological algebras’, Demonstratio Math. 38 (2005), 883–894.Google Scholar
Litvinov, G. L., ‘Hypergroups and hypergroup algebras’, J. Sov. Math. 38 (1987), 1734–1761.Google Scholar
Maghsoudi, S., ‘The space of vector-valued integrable functions under certain locally convex topologies’, Math. Nachr. 286 (2013), 260–271.Google Scholar
Maghsoudi, S. and Nasr-Isfahani, R., ‘Strict topology as a mixed topology on Lebesgue spaces’, Bull. Aust. Math. Soc. 84 (2011), 504–515.CrossRefGoogle Scholar
Maghsoudi, S., Nasr-Isfahani, R. and Rejali, A., ‘The dual of semigroup algebras with certain locally convex topologies’, Semigroup Forum 73 (2006), 367–376.CrossRefGoogle Scholar
Sentilles, F. D., ‘The strict topology on bounded sets’, Pacific J. Math. 34 (1970), 529–540.Google Scholar
Sentilles, F. D. and Taylor, D., ‘Factorization in Banach algebras and the general strict topology’, Trans. Amer. Math. Soc. 142 (1969), 141–152.Google Scholar
Shantha, K. V., ‘The general strict topology in locally convex modules over locally convex algebras II’, Ital. J. Pure Appl. Math. 17 (2005), 21–32.Google Scholar
Shantha, K. V., ‘The general strict topology in locally convex modules over locally convex algebras I’, Ital. J. Pure Appl. Math. 16 (2004), 211–226.Google Scholar
Singh, A. I., ‘L 0∞(G)∗ as the second dual of the group algebra L 1(G) with a locally convex topology’, Michigan Math. J. 46 (1999), 143–150.CrossRefGoogle Scholar
Swartz, C., An Introduction to Functional Analysis, Pure and Applied Mathematics, 157 (Marcel Dekker, New York, 1992).Google Scholar