HYPERPLANES OF FINITE-DIMENSIONAL NORMED SPACES WITH THE MAXIMAL RELATIVE PROJECTION CONSTANT

Abstract

The relative projection constant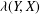${\it\lambda}(Y,X)$ of normed spaces 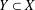$Y\subset X$ is 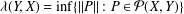${\it\lambda}(Y,X)=\inf \{\Vert P\Vert :P\in {\mathcal{P}}(X,Y)\}$, where 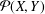${\mathcal{P}}(X,Y)$ denotes the set of all continuous projections from 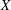$X$ onto 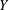$Y$. By the well-known result of Bohnenblust, for every $n$-dimensional normed space 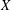$X$ and a subspace 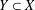$Y\subset X$ of codimension one, 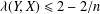${\it\lambda}(Y,X)\leq 2-2/n$. The main goal of the paper is to study the equality case in the theorem of Bohnenblust. We establish an equivalent condition for the equality 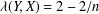${\it\lambda}(Y,X)=2-2/n$ and present several applications. We prove that every three-dimensional space has a subspace with the projection constant less than 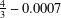$\frac{4}{3}-0.0007$. This gives a nontrivial upper bound in the problem posed by Bosznay and Garay. In the general case, we give an upper bound for the number of (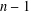$n-1$)-dimensional subspaces with the maximal relative projection constant in terms of the facets of the unit ball of 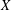$X$. As a consequence, every $n$-dimensional normed space 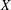$X$ has an (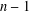$n-1$)-dimensional subspace 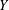$Y$ with 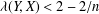${\it\lambda}(Y,X)<2-2/n$. This contrasts with the separable case in which it is possible that every hyperplane has a maximal possible projection constant.