Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T17:11:25.721Z Has data issue: false hasContentIssue false
  • English
  • Français

A HYPERSTABILITY RESULT FOR THE CAUCHY EQUATION

Part of: Equations and inequalities involving nonlinear operators Nonlinear operators and their properties

Published online by Cambridge University Press:  22 August 2013

JANUSZ BRZDĘK
JANUSZ BRZDĘK*
Affiliation:
Department of Mathematics, Pedagogical University, Podchorążych 2, PL-30-084 Kraków, Poland email jbrzdek@up.krakow.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

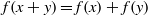We prove a hyperstability result for the Cauchy functional equation $f(x+ y)= f(x)+ f(y)$, which complements some earlier stability outcomes of J. M. Rassias. As a consequence, we obtain the slightly surprising corollary that for every function 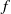$f$, mapping a normed space 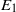${E}_{1} $ into a normed space 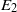${E}_{2} $, and for all real numbers 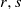$r, s$ with 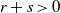$r+ s\gt 0$ one of the following two conditions must be valid:

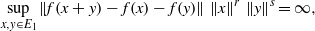$$\begin{eqnarray*}\displaystyle \sup _{x, y\in E_{1}}\Vert f(x+ y)- f(x)- f(y)\Vert \hspace{0.167em} \mathop{\Vert x\Vert }\nolimits ^{r} \hspace{0.167em} \mathop{\Vert y\Vert }\nolimits ^{s} = \infty , &&\displaystyle\end{eqnarray*}$$
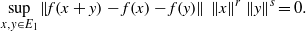$$\begin{eqnarray*}\displaystyle \sup _{x, y\in E_{1}}\Vert f(x+ y)- f(x)- f(y)\Vert \hspace{0.167em} \mathop{\Vert x\Vert }\nolimits ^{r} \hspace{0.167em} \mathop{\Vert y\Vert }\nolimits ^{s} = 0. &&\displaystyle\end{eqnarray*}$$
 In particular, we present a new method for proving stability for functional equations, based on a fixed point theorem.

Keywords

hyperstabilityCauchy equationadditive functionrestricted domain

MSC classification

Secondary: 39B62: Functional inequalities, including subadditivity, convexity, etc. 47H10: Fixed-point theorems 39B82: Stability, separation, extension, and related topics 47H14: Perturbations of nonlinear operators 47J20: Variational and other types of inequalities involving nonlinear operators (general)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 33 - 40
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Aoki, T., ‘On the stability of the linear transformation in Banach spaces’, J. Math. Soc. Japan 2 (1950), 64–66.CrossRefGoogle Scholar
Baker, J. A., ‘The stability of certain functional equations’, Proc. Amer. Math. Soc. 112 (1991), 729–732.CrossRefGoogle Scholar
Borelli Forti, C., ‘Solutions of a nonhomogeneous Cauchy equation’, Radovi Mat. 5 (1989), 213–222.Google Scholar
Bourgin, D. G., ‘Classes of transformations and bordering transformations’, Bull. Amer. Math. Soc. 57 (1951), 223–237.CrossRefGoogle Scholar
Brzdęk, J., Chudziak, J. and Páles, Zs., ‘A fixed point approach to stability of functional equations’, Nonlinear Anal. 74 (2011), 6728–6732.Google Scholar
Brzdęk, J. and Ciepliński, K., ‘A fixed point approach to the stability of functional equations in non-Archimedean metric spaces’, Nonlinear Anal. 74 (2011), 6861–6867.Google Scholar
Cădariu, L. and Radu, V., ‘Fixed point methods for the generalized stability of functional equations in a single variable’, Fixed Point Theory Appl. 2008 (2008), 15 pages; Article ID 749392.Google Scholar
Ciepliński, K., ‘Applications of fixed point theorems to the Hyers–Ulam stability of functional equations—a survey’, Ann. Funct. Anal. 3 (2012), 151–164.CrossRefGoogle Scholar
Davison, T. M. K. and Ebanks, B., ‘Cocycles on cancellative semigroups’, Publ. Math. Debrecen 46 (1995), 137–147.Google Scholar
Ebanks, B., ‘Generalized Cauchy difference functional equations’, Aequationes Math. 70 (2005), 154–176.Google Scholar
Ebanks, B., ‘Generalized Cauchy difference equations. II’, Proc. Amer. Math. Soc. 136 (2008), 3911–3919.CrossRefGoogle Scholar
Ebanks, B., Kannappan, P. L. and Sahoo, P. K., ‘Cauchy differences that depend on the product of arguments’, Glas. Mat. 27 (47) (1992), 251–261.Google Scholar
Ebanks, B., Sahoo, P. and Sander, W., Characterizations of Information Measures (World Scientific, Singapore, 1998).CrossRefGoogle Scholar
Erdös, J., ‘A remark on the paper “On some functional equations” by S. Kurepa’, Glasnik Mat.-Fiz. Astronom. (2) 14 (1959), 3–5.Google Scholar
Fenyö, I. and Forti, G.-L., ‘On the inhomogeneous Cauchy functional equation’, Stochastica 5 (1981), 71–77.Google Scholar
Gajda, Z., ‘On stability of additive mappings’, Int. J. Math. Math. Sci. 14 (1991), 431–434.CrossRefGoogle Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. U.S.A. 27 (1941), 222–224.Google Scholar
Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhäuser, Boston, 1998).Google Scholar
Járai, A., Maksa, Gy. and Páles, Zs., ‘On Cauchy-differences that are also quasisums’, Publ. Math. Debrecen 65 (2004), 381–398.Google Scholar
Jessen, B., Karpf, J. and Thorup, A., ‘Some functional equations in groups and rings’, Math. Scand. 22 (1968), 257–265.Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis, Springer Optimization and its Applications, 48 (Springer, New York, 2011).Google Scholar
Jung, S.-M. and Kim, T.-S., ‘A fixed point approach to the stability of the cubic functional equation’, Bol. Soc. Mat. Mexicana (3) 12 (2006), 51–57.Google Scholar
Jung, S.-M., Kim, T.-S. and Lee, K.-S., ‘A fixed point approach to the stability of quadratic functional equation’, Bull. Korean Math. Soc. 43 (2006), 531–541.CrossRefGoogle Scholar
Jung, Y.-S. and Chang, I.-S., ‘The stability of a cubic functional equation and fixed point alternative’, J. Math. Anal. Appl. 306 (2005), 752–760.Google Scholar
Kuczma, M., An Introduction to the Theory of Functional Equations and Inequalities, Cauchy’s Equation and Jensen’s Inequality, 2nd edn. (Birkhäuser, Basel, 2009).Google Scholar
Maksa, Gy. and Páles, Zs., ‘Hyperstability of a class of linear functional equations’, Acta Math. Acad. Paedagog. Nyházi. (N.S.) 17 (2001), 107–112.Google Scholar
Mirzavaziri, M. and Moslehian, M. S., ‘A fixed point approach to stability of a quadratic equation’, Bull. Braz. Math. Soc. (N.S.) 37 (2006), 361–376.Google Scholar
Radu, V., ‘The fixed point alternative and the stability of functional equations’, Fixed Point Theory 4 (2003), 91–96.Google Scholar
Rassias, J. M., ‘On approximation of approximately linear mappings by linear mappings’, J. Funct. Anal. 46 (1982), 126–130.Google Scholar
Rassias, J. M., ‘On a new approximation of approximately linear mappings by linear mappings’, Discuss. Math. 7 (1985), 193–196.Google Scholar
Rassias, Th. M., ‘On the stability of the linear mapping in Banach spaces’, Proc. Amer. Math. Soc. 72 (1978), 297–300.Google Scholar
Rassias, Th. M., ‘On a modified Hyers–Ulam sequence’, J. Math. Anal. Appl. 158 (1991), 106–113.Google Scholar
Rassias, Th. M. and Semrl, P., ‘On the behavior of mappings which do not satisfy Hyers-Ulam stability’, Proc. Amer. Math. Soc. 114 (1992), 989–993.Google Scholar
Sahoo, P. K. and Kannappan, P., Introduction to Functional Equations (CRC Press, Boca Raton, FL, 2011).Google Scholar
Skof, F., ‘On the stability of functional equations on a restricted domain and related topics’, in: Stability of Mappings of Hyers-Ulam Type, (eds. Rassias, Th. M. and Tabor, J.) (Hadronic Press, Palm Harbor, FL, 1994), 141–151.Google Scholar
Ulam, S. M., Problems in Modern Mathematics (Science Editions, John Wiley & Sons, New York, 1964).Google Scholar