Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T08:41:17.654Z Has data issue: false hasContentIssue false
  • English
  • Français

IDEALS IN DIRECT PRODUCTS OF COMMUTATIVE RINGS

Part of: General commutative ring theory Theory of modules and ideals

Published online by Cambridge University Press:  01 June 2008

D. D. ANDERSON  and
JOHN KINTZINGER
D. D. ANDERSON*
Affiliation:
Department of Mathematics, The University of Iowa, Iowa City, IA, USA (email: dan-anderson@uiowa.edu)
JOHN KINTZINGER
Affiliation:
Department of Mathematics, The University of Iowa, Iowa City, IA, USA (email: johnskintzinger@netscape.net)
*
✉For correspondence; e-mail: dan-anderson@uiowa.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R and S be commutative rings, not necessarily with identity. We investigate the ideals, prime ideals, radical ideals, primary ideals, and maximal ideals of R×S. Unlike the case where R and S have an identity, an ideal (or primary ideal, or maximal ideal) of R×S need not be a ‘subproduct’ I×J of ideals. We show that for a ring R, for each commutative ring S every ideal (or primary ideal, or maximal ideal) is a subproduct if and only if R is an e-ring (that is, for r∈R, there exists er∈R with err=r) (or u-ring (that is, for each proper ideal A of R, 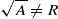)), the Abelian group (R/R2 ,+) has no maximal subgroups).

Keywords

direct product of commutative ringscommutative ringidealprime idealprimary ideale-ringu-ring

MSC classification

Secondary: 13A15: Ideals; multiplicative ideal theory 13C99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 77 , Issue 3 , June 2008 , pp. 477 - 483
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Anderson, D. D., ‘Commutative rings’, in: Multiplicative Ideal Theory in Commutative Algebra, a Tribute to Robert Gilmer (Springer, New York, 2006), pp. 1–20.Google Scholar
[2]Anderson, D. D. and Camillo, V., ‘Subgroups of direct products of groups, ideals and subrings of direct products of rings, and Goursat’s lemma’, Preprint.Google Scholar
[3]Gilmer, R., ‘Eleven non-equivalent conditions on a commutative ring’, Nagoya J. Math. 26 (1966), 174–183.Google Scholar