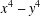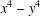Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ratcliffe, Ashleigh
and
Grechuk, Bogdan
2025.
Generalized Fermat equation: A survey of solved cases.
Expositiones Mathematicae,
Vol. 43,
Issue. 4,
p.
125688.