Article contents
Interior regularity of the degenerate Monge-Ampère equation
Published online by Cambridge University Press: 17 April 2009
Abstract
We study interior C1,1 regularity of generalised solutions of the Monge-Ampére equation det D2u = ψ, ψ ≥ 0, on a bounded convex domain Ω in ℝn with u = ϕ on ∂Ω. We prove in particular that u ∈ C1,1(Ω) if either i) ϕ = 0 and ψ1/(n − 1) ∈ C1,1 (Ω) or ii) Ω is C1,1 strongly convex, ϕ ∈ C1,1 (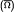 ), ψ1/(n − 1) ∈ C1,1(
), ψ1/(n − 1) ∈ C1,1(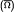 ) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.
) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2003
References
- 7
- Cited by


