Published online by Cambridge University Press: 18 July 2019
This note contains a (short) proof of the following generalisation of the Friedman–Mineyev theorem (earlier known as the Hanna Neumann conjecture): if 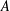 $A$ and
$A$ and 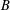 $B$ are nontrivial free subgroups of a virtually free group containing a free subgroup of index
$B$ are nontrivial free subgroups of a virtually free group containing a free subgroup of index  $n$, then
$n$, then 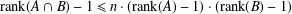 $\text{rank}(A\cap B)-1\leq n\cdot (\text{rank}(A)-1)\cdot (\text{rank}(B)-1)$. In addition, we obtain a virtually-free-product analogue of this result.
$\text{rank}(A\cap B)-1\leq n\cdot (\text{rank}(A)-1)\cdot (\text{rank}(B)-1)$. In addition, we obtain a virtually-free-product analogue of this result.
The work of the first author was supported by the Russian Foundation for Basic Research, project no. 19-01-00591.