Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:12:39.242Z Has data issue: false hasContentIssue false
  • English
  • Français

ISOMETRIES BETWEEN UNIT SPHERES OF THE 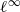${\ell }^{\infty } $-SUM OF STRICTLY CONVEX NORMED SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  28 March 2013

GUANG-GUI DING  and
JIAN-ZE LI
GUANG-GUI DING
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, China email ding_gg@nankai.edu.cn
JIAN-ZE LI*
Affiliation:
School of Science, Tianjin University, Tianjin 30072, China Chern Institute of Mathematics and LPMC, Nankai University, Tianjin 300071, China
*
✉lijianze@yeah.net
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that any surjective isometry between unit spheres of the ${\ell }^{\infty } $-sum of strictly convex normed spaces can be extended to a linear isometry on the whole space, and we solve the isometric extension problem affirmatively in this case.

Keywords

isometric extensionℓ∞-sumstrictly convex normed space

MSC classification

Secondary: 46B04: Isometric theory of Banach spaces 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 369 - 375
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Convey, J., A Course in Functional Analysis, Graduate Texts in Mathematics, 96 (Springer-Verlag, Berlin, 1990).Google Scholar
Ding, G., ‘On isometric extension problem between two unit spheres’, Sci. China Ser. A 52 (10) (2009), 2069–2083.CrossRefGoogle Scholar
Ding, G., ‘The isometric extension of the into mapping from the ${ \mathcal{L} }^{\infty } (\Gamma )$-type space to some normed space $E$’, Illinois J. Math. 51 (2) (2007), 445–453.Google Scholar
Ding, G., ‘The representation of onto isometric mappings between two spheres of ${\ell }^{\infty } $-type spaces and the application on isometric extension problem’, Sci. China 47 (5) (2004), 722–729.CrossRefGoogle Scholar
Fu, X., ‘The isometric extension of the into mapping from the unit sphere ${S}_{1} (E)$ to ${S}_{1} ({\ell }^{\infty } (\Gamma ))$’, Acta Math. Sin., (Engl. Ser.) 24 (9) (2008), 1475–1482.CrossRefGoogle Scholar
Kadets, V. and Martin, M., ‘Extension of isometries between unit spheres of finite-dimensional polyhedral Banach spaces’, J. Math. Anal. Appl. 396 (2012), 441–447.CrossRefGoogle Scholar
Liu, R., ‘On extension of isometries between unit spheres of ${ \mathcal{L} }^{\infty } (\Gamma )$-type space and a Banach space $E$’, J. Math. Anal. Appl. 333 (2007), 959–970.Google Scholar
Tingley, D., ‘Isometries of the unit sphere’, Geom. Dedicata 22 (1987), 371–378.Google Scholar
Wang, R. and Orihara, A., ‘Isometries between the unit spheres of ${\ell }^{1} $-sum of strictly convex normed spaces’, Acta Sci. Natur. Univ. Nankai. 35 (1) (2002), 38–42.Google Scholar