No CrossRef data available.
Published online by Cambridge University Press: 03 March 2022
We show that there exists a continuous function from the unit Lebesgue interval to itself such that for any
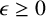 $\epsilon \geq 0$
and any natural number k, any point in its domain has an
$\epsilon \geq 0$
and any natural number k, any point in its domain has an
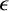 $\epsilon $
-neighbourhood which, when feasible, contains k mutually disjoint extremally scrambled sets of identical Lebesgue measure, homeomorphic to each other. This result enables a satisfying generalisation of Li–Yorke (topological) chaos and suggests an open (difficult) problem as to whether the result is valid for piecewise linear functions.
$\epsilon $
-neighbourhood which, when feasible, contains k mutually disjoint extremally scrambled sets of identical Lebesgue measure, homeomorphic to each other. This result enables a satisfying generalisation of Li–Yorke (topological) chaos and suggests an open (difficult) problem as to whether the result is valid for piecewise linear functions.
Liuchun Deng acknowledges the support of a start-up grant from Yale-NUS College.