Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fabian, M.
1987.
Each weakly countably determined Asplund space admits a Fréchet differentiable norm.
Bulletin of the Australian Mathematical Society,
Vol. 36,
Issue. 3,
p.
367.
Fabian, M.
1987.
On projectional resolution of identity on the duals of certain Banach spaces.
Bulletin of the Australian Mathematical Society,
Vol. 35,
Issue. 3,
p.
363.
Fabian, Marián
and
Troyanski, Stanimir
1990.
A Banach space admits a locally uniformly rotund norm if its dual is a Vašák space.
Israel Journal of Mathematics,
Vol. 69,
Issue. 2,
p.
214.
Valdivia, M.
1990.
Projective resolution of identity inC(K) spaces.
Archiv der Mathematik,
Vol. 54,
Issue. 5,
p.
493.
Schlüchtermann, G.
1991.
Renorming in the space of Bochner integrable functionsL 1(μ,X).
Manuscripta Mathematica,
Vol. 73,
Issue. 1,
p.
397.
Jayne, J. E.
Namioka, I.
and
Rogers, C. A.
1992.
σ‐fragmentable Banach spaces.
Mathematika,
Vol. 39,
Issue. 1,
p.
161.
Argyros, S.
and
Mercourakis, S.
1993.
On Weakly Lindelof Banach Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 2,
Jayne, J. E.
Namioka, I.
and
Rogers, C. A.
1999.
Continuous functions on products of compact Hausdorff spaces.
Mathematika,
Vol. 46,
Issue. 2,
p.
323.
Haydon, R.G.
Jayne, J.E.
Namioka, I.
and
Rogers, C.A.
2000.
Continuous Functions on Totally Ordered Spaces That Are Compact in Their Order Topologies.
Journal of Functional Analysis,
Vol. 178,
Issue. 1,
p.
23.
Zizler, Václav
2003.
Vol. 2,
Issue. ,
p.
1743.
Lajara, S.
Pallarés, A. J.
and
Troyanski, S.
2007.
Some Nonlinear Maps and Renormings of Banach Spaces.
SIAM Journal on Optimization,
Vol. 18,
Issue. 3,
p.
1027.
Kubiś, Wiesław
2009.
Banach spaces with projectional skeletons.
Journal of Mathematical Analysis and Applications,
Vol. 350,
Issue. 2,
p.
758.
Dow, A.
Junnila, H.
and
Pelant, J.
2009.
Chain conditions and weak topologies.
Topology and its Applications,
Vol. 156,
Issue. 7,
p.
1327.
Fabian, Marián
Habala, Petr
Hájek, Petr
Montesinos, Vicente
and
Zizler, Václav
2011.
Banach Space Theory.
p.
575.
Hájek, Petr
Kania, Tomasz
and
Russo, Tommaso
2020.
Separated sets and Auerbach systems in Banach spaces.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 10,
p.
6961.
Correa, Claudia
Cúth, Marek
and
Somaglia, Jacopo
2022.
Characterizations of weakly K-analytic and Vašák spaces using projectional skeletons and separable PRI.
Journal of Mathematical Analysis and Applications,
Vol. 515,
Issue. 1,
p.
126389.
Kąkol, Jerzy
Kubiś, Wiesław
López-Pellicer, Manuel
and
Sobota, Damian
2025.
Descriptive Topology in Selected Topics of Functional Analysis.
Vol. 24,
Issue. ,
p.
547.


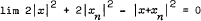 . It is shown that such an equivalent norm exists on every Banach space
. It is shown that such an equivalent norm exists on every Banach space 