Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wu, Qingyan
Fu, Zunwei
and
Petersen, Mark A.
2011.
Sharp Estimates of m‐Linear p‐Adic Hardy and Hardy‐Littlewood‐Pólya Operators.
Journal of Applied Mathematics,
Vol. 2011,
Issue. 1,
Wu, Qing Yan
2012.
Boundedness for commutators of fractional p-adic Hardy operators.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Fu, Zun Wei
Wu, Qing Yan
and
Lu, Shan Zhen
2013.
Sharp estimates of p-adic hardy and Hardy-Littlewood-Pólya operators.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 1,
p.
137.
Wu, Qing Yan
Mi, Ling
and
Fu, Zun Wei
2013.
Boundedness ofp-Adic Hardy Operators and Their Commutators onp-Adic Central Morrey and BMO Spaces.
Journal of Function Spaces and Applications,
Vol. 2013,
Issue. ,
p.
1.
Wu, Qing Yan
and
Fu, Zun Wei
2015.
Hardy-Littlewood-Sobolev Inequalities onp-Adic Central Morrey Spaces.
Journal of Function Spaces,
Vol. 2015,
Issue. ,
p.
1.
Wu, Qing Yan
and
Fu, Zun Wei
2017.
Weighted p-Adic Hardy Operators and Their Commutators on p-Adic Central Morrey Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 40,
Issue. 2,
p.
635.
Li, Xiang
Zhang, Xiran
He, Qianjun
and
Sugimoto, Mitsuru
2021.
Sharp Bounds for Generalized
m
-Linear
n
-Dimensional
p
-Adic Hardy-Littlewood-Pólya Operator.
Journal of Function Spaces,
Vol. 2021,
Issue. ,
p.
1.
He, Qianjun
Li, Xiang
and
Rafeiro, Humberto
2022.
Characterization of Lipschitz Spaces via Commutators of Maximal Function on the p‐Adic Vector Space.
Journal of Mathematics,
Vol. 2022,
Issue. 1,
He, Qianjun
and
Li, Xiang
2023.
Necessary and sufficient conditions for boundedness of commutators of maximal function on the $ p $-adic vector spaces.
AIMS Mathematics,
Vol. 8,
Issue. 6,
p.
14064.
He, Suixin
and
Zhang, Jing
2023.
Boundedness for commutators of rough p-adic fractional Hardy type operators.
Results in Applied Mathematics,
Vol. 19,
Issue. ,
p.
100387.
Dung, K. H.
and
Thuy, P. T. K.
2024.
Rough Hardy-Littlewood Operators on $$p$$-Adic Function Spaces with Variable Exponents.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 16,
Issue. 3,
p.
219.
Ma, Teng
and
Zhou, Jiang
2024.
Weighted multilinear p-adic Hardy operators and commutators on p-adic Herz-type spaces.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 39,
Issue. 3,
p.
554.


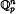 defined by
defined by 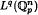 bounded, where 1 <
bounded, where 1 < 