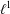Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiménez-Vargas, Antonio
Morales-Campoy, Antonio
Peralta, Antonio M.
and
Ramírez, María Isabel
2019.
The Mazur–Ulam property for the space of complex null sequences.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 4,
p.
799.
Cabello Sánchez, Javier
2019.
A reflection on Tingley's problem and some applications.
Journal of Mathematical Analysis and Applications,
Vol. 476,
Issue. 2,
p.
319.
Becerra Guerrero, Julio
2020.
The Mazur–Ulam property in ℓ∞-sum and c0-sum of strictly convex Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 489,
Issue. 2,
p.
124166.
Cabello Sánchez, Javier
2021.
Linearity of isometries between convex Jordan curves.
Linear Algebra and its Applications,
Vol. 621,
Issue. ,
p.
1.
Banakh, Taras
and
Cabello Sánchez, Javier
2021.
Every non-smooth 2-dimensional Banach space has the Mazur–Ulam property.
Linear Algebra and its Applications,
Vol. 625,
Issue. ,
p.
1.
Banakh, Taras
2022.
Every 2-dimensional Banach space has the Mazur–Ulam property.
Linear Algebra and its Applications,
Vol. 632,
Issue. ,
p.
268.