Article contents
MIN-PHASE-ISOMETRIES IN STRICTLY CONVEX NORMED SPACES
Published online by Cambridge University Press: 22 March 2023
Abstract
Suppose that X and Y are two real normed spaces. A map 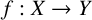 $f:X\rightarrow Y$ is called a min-phase-isometry if it satisfies
$f:X\rightarrow Y$ is called a min-phase-isometry if it satisfies 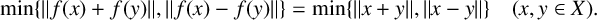 $$ \begin{align*} \min\{\|f(x)+f(y)\|,\|f(x)-f(y)\|\}=\min\{\|x+y\|,\|x-y\|\} \quad (x,y\in X). \end{align*} $$
$$ \begin{align*} \min\{\|f(x)+f(y)\|,\|f(x)-f(y)\|\}=\min\{\|x+y\|,\|x-y\|\} \quad (x,y\in X). \end{align*} $$
We present properties of min-phase-isometries in the case that Y is strictly convex and show that if a min-phase-isometry f (not necessarily surjective) fixes the origin, then it is phase-equivalent to a linear isometry, that is, 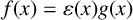 $f(x)=\varepsilon (x)g(x)$ for
$f(x)=\varepsilon (x)g(x)$ for 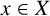 $x\in X$, where
$x\in X$, where 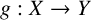 $g:X\rightarrow Y$ is a linear isometry and
$g:X\rightarrow Y$ is a linear isometry and 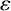 $\varepsilon $ is a map from X to
$\varepsilon $ is a map from X to 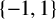 $\{-1,1\}$.
$\{-1,1\}$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 152 - 160
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author is supported by the Natural Science Foundation of China (Grant No. 12271402) and the Natural Science Foundation of Tianjin City (Grant No. 22JCYBJC00420).
References
- 1
- Cited by


