Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T09:48:01.319Z Has data issue: false hasContentIssue false
  • English
  • Français

MORE ON A CERTAIN ARITHMETICAL DETERMINANT

Part of: Elementary number theory Polynomials and matrices Special matrices

Published online by Cambridge University Press:  17 October 2017

ZONGBING LIN  and
SIAO HONG
ZONGBING LIN
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, PR China School of Mathematics and Computer Science, Panzhihua University, Panzhihua 617000, PR China email zongbinglin@sohu.com
SIAO HONG*
Affiliation:
Center for Combinatorics, Nankai University, Tianjin 300071, PR China email sahongnk@gmail.com
*
✉sahongnk@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 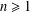$n\geq 1$ be an integer and 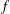$f$ be an arithmetical function. Let 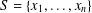$S=\{x_{1},\ldots ,x_{n}\}$ be a set of $n$ distinct positive integers with the property that 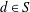$d\in S$ if 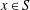$x\in S$ and 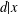$d|x$. Then 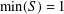$\min (S)=1$. Let 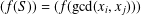$(f(S))=(f(\gcd (x_{i},x_{j})))$ and 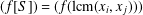$(f[S])=(f(\text{lcm}(x_{i},x_{j})))$ denote the 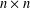$n\times n$ matrices whose 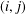$(i,j)$-entries are 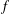$f$ evaluated at the greatest common divisor of 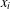$x_{i}$ and 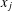$x_{j}$ and the least common multiple of 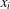$x_{i}$ and 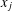$x_{j}$, respectively. In 1875, Smith [‘On the value of a certain arithmetical determinant’, Proc. Lond. Math. Soc. 7 (1875–76), 208–212] showed that 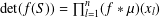$\det (f(S))=\prod _{l=1}^{n}(f\ast \unicode[STIX]{x1D707})(x_{l})$, where 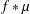$f\ast \unicode[STIX]{x1D707}$ is the Dirichlet convolution of 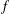$f$ and the Möbius function 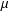$\unicode[STIX]{x1D707}$. Bourque and Ligh [‘Matrices associated with classes of multiplicative functions’, Linear Algebra Appl. 216 (1995), 267–275] computed the determinant 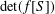$\det (f[S])$ if 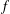$f$ is multiplicative and, Hong, Hu and Lin [‘On a certain arithmetical determinant’, Acta Math. Hungar. 150 (2016), 372–382] gave formulae for the determinants 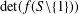$\det (f(S\setminus \{1\}))$ and 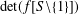$\det (f[S\setminus \{1\}])$. In this paper, we evaluate the determinant 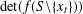$\det (f(S\setminus \{x_{t}\}))$ for any integer $t$ with 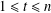$1\leq t\leq n$ and also the determinant 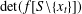$\det (f[S\setminus \{x_{t}\}])$ if 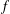$f$ is multiplicative.

Keywords

factor-closed setsquarefree integerarithmetical functionDirichlet convolutionSmith’s determinant

MSC classification

Primary: 11C20: Matrices, determinants
Secondary: 11A05: Multiplicative structure; Euclidean algorithm; greatest common divisors 15B36: Matrices of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 15 - 25
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The research was partially supported partially by National Science Foundation of China Grant Nos. 11371260, 11771304 and 11671218.

References

Altinisik, E., Sagan, B. E. and Tuglu, N., ‘GCD matrices, posets, and nonintersecting paths’, Linear Multilinear Algebra 53 (2005), 75–84.CrossRefGoogle Scholar
Apostol, T. M., ‘Arithmetical properties of generalized Ramanujan sums’, Pacific J. Math. 41 (1972), 281–293.CrossRefGoogle Scholar
Bourque, K. and Ligh, S., ‘Matrices associated with multiplicative functions’, Linear Algebra Appl. 216 (1995), 267–275.CrossRefGoogle Scholar
Codecá, P. and Nair, M., ‘Calculating a determinant associated with multiplicative functions’, Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. 5 (2002), 545–555.Google Scholar
Haukkanen, P., ‘Higher-dimensional GCD matrices’, Linear Algebra Appl. 170 (1992), 53–63.CrossRefGoogle Scholar
Haukkanen, P., Wang, J. and Sillanpää, J., ‘On Smith’s determinant’, Linear Algebra Appl. 258 (1997), 251–269.CrossRefGoogle Scholar
Hilberdink, T., ‘Determinants of multiplicative Toeplitz matrices’, Acta Arith. 125 (2006), 265–284.CrossRefGoogle Scholar
Hong, S. A., Hu, S. N. and Hong, S. F., ‘Multiple gcd-closed sets and determinants of matrices associated with arithmetic functions’, Open Math. 14 (2016), 146–155.CrossRefGoogle Scholar
Hong, S. A., Hu, S. N. and Lin, Z. B., ‘On a certain arithmetical determinant’, Acta Math. Hungar. 150 (2016), 372–382.CrossRefGoogle Scholar
Hong, S. F., Li, M. and Wang, B., ‘Hyperdeterminants associated with multiple even functions’, Ramanujan J. 34 (2014), 265–281.CrossRefGoogle Scholar
Hong, S. F. and Loewy, R., ‘Asymptotic behavior of the smallest eigenvalue of matrices associated with completely even functions (mod r)’, Int. J. Number Theory 7 (2011), 1681–1704.CrossRefGoogle Scholar
Korkee, I. and Haukkanen, P., ‘On meet matrices with respect to reduced, extended and exchanged sets’, JP J. Algebra Number Theory Appl. 4 (2004), 559–575.Google Scholar
Mattila, M., ‘On the eigenvalues of combined meet and join matrices’, Linear Algebra Appl. 466 (2015), 1–20.CrossRefGoogle Scholar
McCarthy, P. J., ‘A generalization of Smith’s determinant’, Canad. Math. Bull. 29 (1986), 109–113.CrossRefGoogle Scholar
Smith, H. J. S., ‘On the value of a certain arithmetical determinant’, Proc. Lond. Math. Soc. 7 (1875–76), 208–212.Google Scholar
Weber, M. J. G., ‘An arithmetical approach to the convergence problem of series of dilated functions and its connection with the Riemann zeta function’, J. Number Theory 162 (2016), 137–179.CrossRefGoogle Scholar
Yamasaki, Y., ‘Arithmetical properties of multiple Ramanujan sums’, Ramanujan J. 21 (2010), 241–261.CrossRefGoogle Scholar