Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:19:01.526Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICITIES OF EIGENVALUES OF THE DIFFUSION OPERATOR WITH RANDOM JUMPS FROM THE BOUNDARY

Part of: Ordinary differential operators Markov processes General theory of linear operators

Published online by Cambridge University Press:  28 November 2018

JUN YAN Open the ORCID record for JUN YAN [Opens in a new window]  and
GUOLIANG SHI Open the ORCID record for GUOLIANG SHI [Opens in a new window]
JUN YAN*
Affiliation:
School of Mathematics, Tianjin University, Tianjin, 300354, PR China email jun.yan@tju.edu.cn
GUOLIANG SHI
Affiliation:
School of Mathematics, Tianjin University, Tianjin, 300354, PR China email glshi@tju.edu.cn
*
✉jun.yan@tju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with a non-self-adjoint differential operator which is associated with a diffusion process with random jumps from the boundary. Our main result is that the algebraic multiplicity of an eigenvalue is equal to its order as a zero of the characteristic function 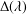$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D706})$. This is a new criterion for determining the multiplicities of eigenvalues for concrete operators.

Keywords

diffusioneigenvaluenon-self-adjointmultiplicity

MSC classification

Primary: 34L15: Eigenvalues, estimation of eigenvalues, upper and lower bounds
Secondary: 47A10: Spectrum, resolvent 60J60: Diffusion processes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 101 - 113
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The work was done at the University of Vienna while the first author was visiting the Fakultät für Mathematik, supported by the China Scholarship Council. This research was also supported by the National Natural Science Foundation of China (Grant No. 11601372) and the Science and Technology Research Project of Higher Education in Hebei Province (Grant No. QN2017044).

References

Arendt, W., Kunkel, S. and Kunze, M., ‘Diffusion with nonlocal boundary conditions’, J. Funct. Anal. 270 (2016), 2483–2507.Google Scholar
Ben-Ari, I., ‘Coupling for drifted Brownian motion on an interval with redistribution from the boundary’, Electron. Commun. Probab. 19 (2014), 1–11.Google Scholar
Ben-Ari, I. and Pinsky, R. G., ‘Spectral analysis of a family of second-order elliptic operators with nonlocal boundary condition indexed by a probability measure’, J. Funct. Anal. 251 (2007), 122–140.Google Scholar
Ben-Ari, I. and Pinsky, R. G., ‘Ergodic behavior of diffusions with random jumps from the boundary’, Stochastic Process. Appl. 119 (2009), 864–881.Google Scholar
Feller, W., ‘Diffusion processes in one dimension’, Trans. Amer. Math. Soc. 17 (1954), 1–31.Google Scholar
Grigorescu, I. and Kang, M., ‘Brownian motion on the figure eight’, J. Theoret. Probab. 15 (2002), 817–844.Google Scholar
Grigorescu, I. and Kang, M., ‘Ergodic properties of multidimensional Brownian motion with rebirth’, Electron. J. Probab. 12 (2007), 1299–1322.Google Scholar
Halmos, P. R., Finite-Dimensional Vector Spaces (Springer, New York, 1974).Google Scholar
Kato, T., Perturbation Theory for Linear Operators (Springer, Berlin, 1966).Google Scholar
Kolb, M. and Krejčiřík, D., ‘Spectral analysis of the diffusion operator with random jumps from the boundary’, Math. Z. 284 (2016), 877–900.Google Scholar
Kolb, M. and Wubker, A., ‘On the spectral gap of Brownian motion with jump boundary’, Electron. J. Probab. 16 (2011), 1214–1237.Google Scholar
Kolb, M. and Wubker, A., ‘Spectral analysis of diffusions with jump boundary’, J. Funct. Anal. 261 (2011), 1992–2012.Google Scholar
Leung, Y. J., Li, W. V. and Rakesh, ‘Spectral analysis of Brownian motion with jump boundary’, Proc. Amer. Math. Soc. 136 (2008), 4427–4436.Google Scholar
Taylor, A. E. and Lay, D. C., Introduction to Functional Analysis (Wiley, New York, 1980).Google Scholar
Zettl, A., Sturm–Liouville Theory (American Mathematical Society, Providence, RI, 2005).Google Scholar