Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T21:11:47.296Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MULTIPLIER ALGEBRA AND BSE PROPERTY OF THE DIRECT SUM OF BANACH ALGEBRAS

Part of: Locally compact groups and their algebras Commutative Banach algebras and commutative topological algebras

Published online by Cambridge University Press:  07 February 2013

ZEINAB KAMALI  and
MAHMOOD LASHKARIZADEH BAMI
ZEINAB KAMALI*
Affiliation:
Department of Mathematics, Faculty of Science, University of Isfahan, Isfahan, Iran email lashkari@sci.ui.ac.ir
MAHMOOD LASHKARIZADEH BAMI
Affiliation:
Department of Mathematics, Faculty of Science, University of Isfahan, Isfahan, Iran email lashkari@sci.ui.ac.ir
*
✉ze.kamali@sci.ui.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The notion of BSE algebras was introduced and first studied by Takahasi and Hatori and later studied by Kaniuth and Ülger. This notion depends strongly on the multiplier algebra 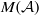$M( \mathcal{A} )$ of a commutative Banach algebra 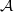$ \mathcal{A} $. In this paper we first present a characterisation of the multiplier algebra of the direct sum of two commutative semisimple Banach algebras. Then as an application we show that 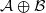$ \mathcal{A} \oplus \mathcal{B} $ is a BSE algebra if and only if 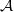$ \mathcal{A} $ and 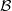$ \mathcal{B} $ are BSE. We also prove that if the algebra 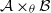$ \mathcal{A} \hspace{0.167em} {\mathop{\times }\nolimits}_{\theta } \hspace{0.167em} \mathcal{B} $ with 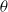$\theta $-Lau product is a BSE algebra and 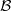$ \mathcal{B} $ is unital then 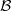$ \mathcal{B} $ is a BSE algebra. We present some examples which show that the BSE property of 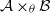$ \mathcal{A} \hspace{0.167em} {\mathop{\times }\nolimits}_{\theta } \hspace{0.167em} \mathcal{B} $ does not imply the BSE property of 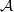$ \mathcal{A} $, even in the case where 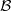$ \mathcal{B} $ is unital.

Keywords

commutative Banach algebramultiplier algebraBSE algebradirect sum

MSC classification

Secondary: 46J05: General theory of commutative topological algebras 22D15: Group algebras of locally compact groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 2 , October 2013 , pp. 250 - 258
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Baggett, L. and Taylor, K., ‘A sufficient condition for the complete reducibility of the regular representation’, J. Funct. Anal. 34 (1979), 250–265.CrossRefGoogle Scholar
Bochner, S., ‘A theorem on Fourier–Stieltjes integrals’, Bull. Amer. Math. Soc. 40 (1934), 271–276.CrossRefGoogle Scholar
Eberlein, W. F., ‘Characterizations of Fourier–Stieltjes transforms’, Duke. Math. J. 22 (1955), 465–468.CrossRefGoogle Scholar
Fattahi, A., ‘Multiplier on character amenable Banach algebras’, Int. Math. Forum 42 (2010), 2085–2091.Google Scholar
Figà-Talamanca, A., ‘Positive definite functions which vanish at infinity’, Pacific J. Math. 69 (1977), 355–363.CrossRefGoogle Scholar
Jones, C. A. and Lahr, C. D., ‘Weak and norm approximate identities are different’, Pacific J. Math. 72 (1977), 99–104.CrossRefGoogle Scholar
Kamali, Z. and Nemati, M., ‘On $n$-ideal amenability of certain Banach algebras’, Bull. Aust. Math. Soc. 86 (2012), 90–99.CrossRefGoogle Scholar
Kaniuth, E. and Ülger, A., ‘The Bochner–Schoenberg–Eberlein property for commutative Banach algebras, especially Fourier and Fourier–Stieltjes algebras’, Trans. Amer. Math. Soc. 362 (2010), 4331–4356.CrossRefGoogle Scholar
Larsen, R., An Introduction to the Theory of Multipliers (Springer, New York, 1971).CrossRefGoogle Scholar
Lau, A. T.-M., ‘Analysis on a class of Banach algebras with applications to harmonic analysis on locally compact groups and semigroups’, Fund. Math. 118 (1983), 161–175.Google Scholar
Rudin, W., Fourier Analysis on Groups (Wiley Interscience, New York, 1984).Google Scholar
Sangani Monfared, M., ‘On certain products of Banach algebras with applications to harmonic analysis’, Studia Math. 178 (2007), 277–294.CrossRefGoogle Scholar
Schoenberg, I. J., ‘A remark on the preceeding note by Bochner’, Bull. Amer. Math. Soc. 40 (1934), 277–278.CrossRefGoogle Scholar
Takahasi, S.-E. and Hatori, O., ‘Commutative Banach algebras which satisfy a Bochner–Schoenberg–Eberlin-type theorem’, Proc. Amer. Math. Soc. 110 (1990), 149–158.Google Scholar
Takahasi, S.-E. and Hatori, O., ‘Commutative Banach algebras and BSE-inequalities’, Math. Japonica 37 (1992), 47–52.Google Scholar
Zaime, Y., ‘Opérateurs de convolution d’image fermé et unité approchés’, Bull. Sci. Math 2e Sèr. 99 (1975), 65–74.Google Scholar