Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T19:35:38.659Z Has data issue: false hasContentIssue false
  • English
  • Français

NATURAL PARTIAL ORDER IN SEMIGROUPS OF TRANSFORMATIONS WITH INVARIANT SET

Part of: Semigroups

Published online by Cambridge University Press:  22 May 2012

LEI SUN  and
LIMIN WANG
LEI SUN*
Affiliation:
Department of Mathematics, South China Normal University, Guangzhou, Guangdong, 510631, PR China School of Mathematics and Information Science, Henan Polytechnic University, Henan, Jiaozuo, 454003, PR China (email: sunlei97@163.com)
LIMIN WANG
Affiliation:
Department of Mathematics, South China Normal University, Guangzhou, Guangdong, 510631, PR China
*
✉For correspondence; e-mail: sunlei97@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

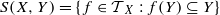Let 𝒯X be the full transformation semigroup on the nonempty set X. We fix a nonempty subset Y of X and consider the semigroup of transformations that leave Y invariant, and endow it with the so-called natural partial order. Under this partial order, we determine when two elements of S(X,Y ) are related, find the elements which are compatible and describe the maximal elements, the minimal elements and the greatest lower bound of two elements. Also, we show that the semigroup S(X,Y ) is abundant.

Keywords

transformation semigroupsnatural orderabundance

MSC classification

Secondary: 20M20: Semigroups of transformations, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 1 , February 2013 , pp. 94 - 107
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2012

Footnotes

This paper is partially supported by National Natural Science Foundation of China (No. 10971086) and Natural Science Foundation of Henan Province (Nos 112300410120, 122300410276).

References

[1]Araujo, J. and Konieczny, J., ‘Semigroups of transformations preserving an equivalence relation and a cross-section’, Comm. Algebra 32 (2004), 1917–1935.CrossRefGoogle Scholar
[2]Fountain, J. B., ‘Abundant semigroups’, Proc. Lond. Math. Soc. (3) 44 (1982), 103–129.CrossRefGoogle Scholar
[3]Honyam, P. and Sanwong, J., ‘Semigroups of transformations with invariant set’, J. Korean Math. Soc. 48 (2011), 289–300.CrossRefGoogle Scholar
[4]Kowol, G. and Mitsch, H., ‘Naturally ordered transformation semigroups’, Monatsh. Math. 102 (1986), 115–138.CrossRefGoogle Scholar
[5]Magill, K. D. Jr., ‘Subsemigroups of S(X)’, Math. Japonica 11 (1966), 109–115.Google Scholar
[6]Mitsch, H., ‘A natural partial order for semigroups’, Proc. Amer. Math. Soc. 97 (1986), 384–388.CrossRefGoogle Scholar
[7]Nenthein, S., Youngkhong, P. and Kemprasit, Y., ‘Regular elements of some transformation semigroups’, Pure Math. Appl. 16 (2006), 307–314.Google Scholar
[8]Paula, M., Marques-Smith, O. and Sullivan, R. P., ‘Partial orders on transformation semigroups’, Monatsh. Math. 140 (2003), 103–118.CrossRefGoogle Scholar
[9]Pei, H. S. and Zhou, H. J., ‘Abundant semigroups of transformations preserving an equivalence relation’, Algebra Colloq. 18 (2011), 77–82.CrossRefGoogle Scholar
[10]Sullivan, R. P., ‘Partial orders on linear transformation semigroups’, Proc. R. Soc. Edinburgh Sect. A-Math. 135 (2005), 413–437.CrossRefGoogle Scholar
[11]Sun, L., Pei, H. S. and Cheng, Z. X., ‘Naturally ordered transformation semigroups preserving an equivalence’, Bull. Aust. Math. Soc. 78 (2008), 117–128.CrossRefGoogle Scholar
[12]Symons, J. S., ‘Some results concerning a transformation semigroup’, J. Aust. Math. Soc. 19 (1975), 413–425.CrossRefGoogle Scholar
[13]Umar, A., ‘On the semigroups of order-decreasing finite full transformations’, Proc. R. Soc. Edinburgh 120A (1992), 129–142.CrossRefGoogle Scholar