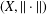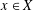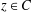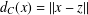Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Zi Hou
Liu, Chun Yan
Zhou, Yu
and
Zhou, Jing
2021.
On Weak Well-posedness of the Nearest Point and Mutually Nearest Point Problems in Banach Spaces.
Acta Mathematica Sinica, English Series,
Vol. 37,
Issue. 8,
p.
1303.