Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T13:26:07.319Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW CONGRUENCE MODULO 25 FOR 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  08 October 2014

ERNEST X. W. XIA
ERNEST X. W. XIA*
Affiliation:
Department of Mathematics, Jiangsu University, Zhenjiang, Jiangsu 212013, PR China email ernestxwxia@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any positive integer $n$, let 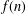$f(n)$ denote the number of 1-shell totally symmetric plane partitions of $n$. Recently, Hirschhorn and Sellers [‘Arithmetic properties of 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc.89 (2014), 473–478] and Yao [‘New infinite families of congruences modulo 4 and 8 for 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc.90 (2014), 37–46] proved a number of congruences satisfied by 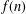$f(n)$. In particular, Hirschhorn and Sellers proved that 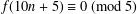$f(10n+5)\equiv 0\ (\text{mod}\ 5)$. In this paper, we establish the generating function of 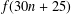$f(30n+25)$ and prove that 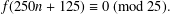$f(250n+125)\equiv 0\ (\text{mod\ 25}).$

Keywords

congruence1-shell totally symmetric plane partitionsTSPP

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 41 - 46
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., Paule, P. and Schneider, C., ‘Plane partitions VI: Stembridge’s TSPP theorem’, Adv. Appl. Math. 34 (2005), 709–739.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).Google Scholar
Blecher, A., ‘Geometry for totally symmetric plane partitions (TSPPs) with self-conjugate main diagonal’, Util. Math. 88 (2012), 223–235.Google Scholar
Fine, N. J., Basic Hypergeometric Series and Applications, Mathematical Surveys and Monographs, 27 (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Hirschhorn, M. D., ‘An identity of Ramanujan, and applications’, in: q-Series from a Contemporary Perspective, Contemporary Mathematics, 254 (American Mathematical Society, Providence, RI, 2000), 229–234.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic properties of 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc. 89 (2014), 473–478.Google Scholar
Stembridge, J. R., ‘The enumeration of totally symmetric plane partitions’, Adv. Math. 111 (1995), 227–243.CrossRefGoogle Scholar
Yao, O. X. M., ‘New infinite families of congruences modulo 4 and 8 for 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc. 90 (2014), 37–46.Google Scholar