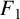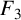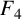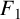NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES $F_1$

Abstract

Liu [‘Supercongruences for truncated Appell series’, Colloq. Math. 158(2) (2019), 255–263] and Lin and Liu [‘Congruences for the truncated Appell series $F_3$ and $F_4$’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed four supercongruences for truncated Appell series. Motivated by their work, we give a new supercongruence for the truncated Appell series $F_{1}$, together with two generalisations of this supercongruence, by establishing its q-analogues.

1. Introduction

In 1880, Appell defined four kinds of double series $F_{1}$ , $F_{2}$ , $F_{3}$ , $F_{4}$ in two variables (see [12, pages 210–211]) by generalising the Gauss hypergeometric series. These four series, called Appell series, are well known in the field of double hypergeometric series.

Based on the definition of the truncated hypergeometric series, Liu [9] introduced the truncated Appell series, defined by

$$ \begin{align*} F_{1} [a;b,b{'} ;c;x,y]_{n}&=\sum_{i=0}^{n} \sum_{j=0}^{n}\frac{(a)_{i+j}(b)_{i} (b{'})_{j}}{(c)_{i+j}} \cdot \frac{x^{i}y^{j}}{i!j!}; \\ F_{2} [a;b,b{'} ;c,c{'};x,y]_{n}&=\sum_{i=0}^{n} \sum_{j=0}^{n}\frac{(a)_{i+j}(b)_{i} (b{'})_{j}}{(c)_{i}(c{'})_{j}} \cdot \frac{x^{i}y^{j}}{i!j!}; \\ F_{3} [a,a{'};b,b{'} ;c;x,y]_{n}&=\sum_{i=0}^{n} \sum_{j=0}^{n}\frac{(a)_{i}(a{'})_{j}(b)_{i} (b{'})_{j}}{(c)_{i+j}} \cdot \frac{x^{i}y^{j}}{i!j!}; \\ F_{4} [a;b;c,c{'};x,y]_{n}&=\sum_{i=0}^{n} \sum_{j=0}^{n}\frac{(a)_{i+j}(b)_{i+j}}{(c)_{i}(c{'})_{j}} \cdot \frac{x^{i}y^{j}}{i!j!}, \end{align*} $$

where $(x)_n$ is the shifted factorial $(x)_{n} =x(x+1)\cdots (x+n-1)$ with $n \in \mathbb {Z}^{+}$ and $(x)_{0}=1$ .

In [9], Liu confirmed two congruences for the truncated Appell series $F_{1}$ and $F_{2}$ by using combinatorial identities: for any prime $p \ge $ 5, modulo $p^{2}$ ,

$$ \begin{align*} F_1[\tfrac12;\tfrac12,\tfrac12;1;1,1]_{(p-1)/2} &\equiv 1 \\ F_2[\tfrac12;\tfrac12,\tfrac12;1,1;1,1]_{(p-1)/2} &\equiv\begin{cases} -\Gamma_p(\frac{1}{4})^{4} & \mbox{if } p \equiv 1 \pmod{4}, \\ 0 & \mbox{if } p \equiv 3 \pmod{4}. \end{cases} \end{align*} $$

Later, Lin and Liu [8] studied congruence properties of the truncated Appell series $F_{3}$ and $F_{4}$ : for any prime $p \ge $ 5, modulo $p^{2}$ ,

(1.1) $$ \begin{align} F_3[\tfrac12,\tfrac12;\tfrac12,\tfrac12;1;1,1]_{(p-1)/2} &\equiv (-1)^{{p-1}/{2}},\\F_4[\tfrac12;\tfrac12;1,1;1,1]_{(p-1)/2} &\equiv \begin{cases} (-1)^{{p+1}/{2} }\Gamma_p(\frac{1}{6})^{2}\Gamma_p(\frac{1}{3}) ^{2} & \mbox{if } p \equiv 1 \pmod{3}, \\ 0 & \mbox{if } p \equiv 2 \pmod{3}.\notag \end{cases} \end{align} $$

Here $\Gamma _p$ is the p-adic Gamma function for p an odd prime, given by

$$ \begin{align*} \Gamma_p(\alpha)=\lim_{n\rightarrow \alpha}(-1)^n\prod_{\substack{0<j<n\\ p\nmid j}}j \end{align*} $$

for $\alpha \in \mathbb Z_p$ , and $\mathbb Z_p$ denotes the ring of all p-adic integers.

Recently, Wang and Yu [14] gave a generalisation of (1.1) with one free parameter d by establishing a q-supercongruence: for n a positive odd integer and d an integer with $n\ge \max \{2d+1, 1-2d \}$ , modulo $\Phi _n(q)^{4}$ ,

$$ \begin{align*} &\sum_{i=0}^{{(n-1)}/{2}-d}\sum_{j=0}^{{(n-1)}/{2}+d}\frac{(q^{2d+1};q^2)_{i}^2(q^{1-2d};q^2)_{j}^2}{(q^2;q^2)_i(q^2;q^2)_j(q^2;q^2)_{i+j}}q^{2ij-4di+4dj} \\ & \equiv \left \{\begin{aligned} & (-1)^{{(n-1)}/{2}}q^{{(1-n^2)}/{4}}, & d = 0, \\ & (1-q^n)^2q^{|d|(2+3|d|-n)-n+{(1-n^2)}/{4}}\sum_{k=1}^{2|d|}(-1)^{k-|d|+{(n-1)}/{2}}q^{k^2-k}H_k(-2|d|-1)\\ & \quad\quad\times\frac{(q^{n+2|d|-2k+1};q^2)_k(q^{4|d|-2k+2};q^2)_{(n-2|d|-1)/2}}{(q^2;q^2)_k(q^2;q^2)_{(n-2|d|-1)/2}}, & d\neq 0,\end{aligned}\right.\end{align*} $$

where $H_k(x)=\sum _{t=1}^{k}{q^{2t+x}}/{(1-q^{2t+x})^2}$ , $k \in \mathbb {Z}^{+}$ . The q-shifted factorial is defined by $(a;q)_{0}=1$ and $(a;q)_{n}=(1-a)(1-aq)\cdots (1-aq^{n-1})$ with $n \in \mathbb {Z}^{+}$ ; the q-integer is $[n]=[n]_{q}=(q^n-1)/(q-1)$ and $\Phi _n(q)$ denotes the nth cyclotomic polynomial in q, which can be factorised as

$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\ \gcd(n,k)=1}}(q-\zeta^k) \end{align*} $$

with $\zeta $ a primitive nth root of unity. In addition, the q-binomial coefficient is defined by

$$ \begin{align*} {x\brack k}={x\brack k}_{q} = \begin{cases} & \frac{(q^{1+x-k};q)_k}{(q;q)_k}, & k \geq 0, & \\ & 0, & k < 0. & \end{cases}\end{align*} $$

Inspired by the work mentioned above, and recent progress on congruences and q-congruences (see [2–7, 10, 11, 13–15]), we continue the study of congruences for the truncated Appell series $F_{1}$ and obtain new results.

Theorem 1.1. Let p be a prime with $p \equiv 1\pmod {4}$ . Then

$$ \begin{align*} F_1[\tfrac12;\tfrac14,\tfrac14;1;1,1]_{(p-1)/2} \equiv 1 \pmod {p^2}. \end{align*} $$

We establish two generalised q-analogues of Theorem 1.1.

Theorem 1.2. Let d and n be positive integers with $n\equiv 1 \pmod {2d}$ . Then, modulo $\Phi _n(q)^{2}$ ,

(1.2) $$ \begin{align} \sum_{i=0}^{{(n-1)}/{d}}\sum_{j=0}^{{(n-1)}/{d}}\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj} \equiv \begin{bmatrix} -\dfrac{2}{d} \\[2mm] \dfrac{n-1}{d} \end{bmatrix} _{q^{2d}}q^{{(2n^{2}-2)}/{d}}. \end{align} $$

Theorem 1.3. Let d be an even positive integer and n a positive integer with $n \equiv d-1 \pmod {2d}$ . Then, modulo $\Phi _n(q)^{2}$ ,

$$ \begin{align*} &\sum_{i=0}^{{(n-(d-1))}/{d}}\sum_{j=0}^{{(n-(d-1))}/{d}}\frac{(q^{2d-2};q^{2d})_{i+j}(q^{d-1};q^{2d})_{i}(q^{d-1};q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}} q^{3di-i+2dj+2d-4} \notag \\ &\qquad \equiv \begin{bmatrix} \dfrac{2}{d} -2 \\[2mm] \dfrac{n-(d-1)}{d} \end{bmatrix} _{q^{2d}}q^{{(2n^{2}-2)}/{d}}. \end{align*} $$

Letting n be a prime p and then taking $q \rightarrow 1$ in Theorems 1.2 and 1.3 gives the following conclusions.

Corollary 1.4. Let p be a prime and d a positive integer with $p \equiv 1 \pmod {2d}$ . Then

$$ \begin{align*} F_1\bigg[\frac1d;\frac{1}{2d},\frac{1}{2d};1;1,1\bigg]_{(p-1)/d} \equiv \begin{pmatrix} -\dfrac{2}{d} \\[2mm] \dfrac{p-1}{d} \end{pmatrix} \pmod {p^2}. \end{align*} $$

Corollary 1.5. Let p be a prime and d an even positive integer with $p \equiv d-1 \pmod {2d}$ . Then

$$ \begin{align*} F_1\bigg[\frac{d-1}{d};\frac{d-1}{2d},\frac{d-1}{2d};1;1,1\bigg]_{(p-(d-1))/d} \equiv \begin{pmatrix} \dfrac{2}{d}-2 \\[2mm] \dfrac{p-(d-1)}{d} \end{pmatrix} \pmod {p^2}. \end{align*} $$

Theorem 1.1 is the special case $d=2$ of Corollaries 1.4 and 1.5. In the following two sections, we give the proofs of Theorems 1.2 and 1.3.

The famous q-Chu–Vandermonde identity [1, (1.5.2)] can be converted to

(1.3) $$ \begin{align}\sum_{k=0}^{n} {x\brack k} {y\brack n-k}q^{(x-k)(n-k)} ={x+y\brack n}, \end{align} $$

and this will be frequently used in our proofs.

2. Proof of Theorem 1.2

Since $n \equiv 1\pmod {2d}$ , we have $\gcd (2d,n) = 1$ . Hence, $(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}$ is relatively prime to $\Phi _n(q)$ for $0 \le i+j \le n-1$ . Also, $(q^{2};q^{2d})_{i+j} \equiv $ 0 (mod $\Phi _n(q)$ ) for ${(n-1}/{d} +1\le i\le {2(n-1)}/{d}$ and $(q;q^{2d})_{i} \equiv $ 0 (mod $\Phi _n(q)$ ) for ${(n-1)}/{2d} +1\le i\le {2(n-1)}/{d}$ . So,

$$ \begin{align*} \frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}} \equiv 0 \pmod {\Phi_n(q)^{2}} \quad \text{when } \frac{n-1}{d} +1\le i,i+j\le \frac{2(n-1)}{d}. \end{align*} $$

By symmetry, also

$$ \begin{align*} \frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{j}} \equiv 0 \pmod {\Phi_n(q)^{2}} \quad \text{when } \frac{n-1}{d} +1\le j,i+j\le \frac{2(n-1)}{d}. \end{align*} $$

Now, the left-hand side of (1.2) can be evaluated as

$$ \begin{align*} &\sum_{i=0}^{{(n-1)}/{d}} \sum_{j=0}^{({n-1)}/{d}}\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj}\notag\ \\[5pt] &\qquad\equiv \sum_{i=0}^{{(n-1)}/{d}}\sum_{j=0}^{{(n-1)}/{d}}\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj}\notag\ \\[5pt] &\qquad\quad +\sum_{{(n-1)}/{d}+1\le i,i+j\le {2(n-1)}/{d}}^{ }\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj} \notag\ \\[5pt] &\qquad\quad +\sum_{{(n-1)}/{d}+1\le j,i+j\le {2(n-1)}/{d}}^{ }\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj} \notag\ \\[5pt]&\qquad\equiv \sum_{0 \le i+j \le {2(n-1)}/{d}}^{}\frac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj}\notag\ \\ &\qquad\equiv \sum_{m=0}^{{2(n-1)}/{d} } \begin{bmatrix} -\dfrac{1}{d} \\ m \end{bmatrix}_{q^ {2d}}\sum_{i=0}^{m} \begin{bmatrix} -\dfrac{1}{2d} \\ i \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{1}{2d} \\ m-i \end{bmatrix}_{q^{2d}}q^{i+3m+2di^{2}-2dmi+2dm^{2}} \notag \\[4pt] &\qquad \equiv \sum_{m=0}^{{2(n-1)}/{d} } \begin{bmatrix} -\dfrac{1}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{1}{d} \\ m \end{bmatrix}_{q^{2d}}q^{4m+2dm^{2}} \pmod {\Phi_n(q)^{2}}, \end{align*} $$

where we have performed the replacement $m=i+j$ and applied the q-Chu–Vandermonde identity (1.3).

When ${(n-1)}/{d} < m< n$ ,

$$ \begin{align*} \begin{bmatrix}-\dfrac{1}{d}\\[1mm] m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{1}{d} \\[1mm] m \end{bmatrix}_{q^{2d}} = \dfrac{(q^{2};q^{2d})^{2}_{m}}{(q^{2d};q^{2d})^{2}_{m}}q^{-4d\binom{m}{2}-4m} \equiv 0 \pmod {\Phi_n(q)^{2}}, \end{align*} $$

for $(q^{2};q^{2d})_{m} \equiv $ 0 (mod $\Phi _n(q)$ ), and $(q^{2d};q^{2d})_{m}$ is relatively prime to $\Phi _n(q)$ . Therefore, modulo $\Phi _n(q)^{2}$ , the left-hand side of (1.2) can be simplified as

$$ \begin{align*} \sum_{i=0}^{{(n-1)}/{d}}\sum_{j=0}^{{(n-1)}/{d}}\dfrac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj} \equiv \!\sum_{m=0}^{{(n-1)}/{d} } \begin{bmatrix} -\dfrac{1}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{1}{d} \\ m \end{bmatrix}_{q^{2d}}q^{4m+2dm^{2}}\!. \end{align*} $$

lt is easy to check that

$$ \begin{align*} (1-q^{n-t})(1-q^{n+t})+(1-q^{t})^{2}q^{n-t} = (1-q^{n})^{2}, \end{align*} $$

from which we deduce

$$ \begin{align*} &\begin{bmatrix} \dfrac{n-1}{d} _{} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} \dfrac{n-(d-1)}{d} +m_{} \\ m \end{bmatrix}_{q^{2d}} =\dfrac{1}{(q^{2d};q^{2d})^{2}_{m}} \prod_{t=1}^{m}(1-q^{2n+(2+2td-2d)})(1-q^{2n-(2+2td-2d)}) \notag \\[4pt] &\quad=\dfrac{1}{(q^{2d};q^{2d})^{2}_{m}}\prod_{t=1}^{m}\big\{(1-q^{2n})^{2}-(1-q^{2n-(2+2td-2d)})^{2}q^{2n-(2+2td-2d)}\big\} \notag \\[4pt] &\quad \equiv (-1)^{m}\dfrac{(q^{2};q^{2d})^{2}_{m}}{(q^{2d};q^{2d})^{2}_{m}}q^{(2n-dm+d-2)m} \notag \\[4pt] &\quad\equiv (-1)^{m}\begin{bmatrix} -\dfrac{1}{d} _{} \\ m \end{bmatrix}_{q^{2d}}\begin{bmatrix} -\dfrac{1}{d} _{} \\ m \end{bmatrix}_{q^{2d}}q^{2nm+dm^{2}-dm+2m} \pmod{\Phi_n(q)^{2}}. \end{align*} $$

Thus, the left-hand of (1.2) becomes

$$ \begin{align*} &\sum_{i=0}^{{(n-1)}/{d}} \sum_{j=0}^{{(n-1)}/{d}}\dfrac{(q^{2};q^{2d})_{i+j}(q;q^{2d})_{i}(q;q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{i+2di+2dj}\\[5pt] &\qquad \equiv \sum_{m=0}^{{(n-1)}/{d} } (-1)^{m} \begin{bmatrix} \dfrac{n-1}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} \dfrac{n-(d-1)}{d} +m \\ m \end{bmatrix}_{q^{2d}}q^{(2+d-2n)m+dm^{2}} \\[5pt] &\qquad\equiv \sum_{m=0}^{{(n-1)}/{d} } \begin{bmatrix} \dfrac{n-1}{d} \\[2mm] \dfrac{n-1}{d}-m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{n-(d-1)}{d}-1 \\ m \end{bmatrix}_{q^{2d}}q^{2dm^{2}+4m}\\[5pt] &\qquad\equiv \begin{bmatrix} -\dfrac{2}{d} \\[2mm] \dfrac{n-1}{d} \end{bmatrix} _{q^{2d}}q^{{(2n^{2}-2)}/{d}} \pmod{\Phi_n(q)^{2}}, \end{align*} $$

where we have used the q-Chu–Vandermonde identity (1.3) in the last line. This completes the proof of Theorem 1.2.

3. Proof of Theorem 1.3

The proof of Thereom 1.3 is very similar to the proof of Thereom 1.2. We give a sketch of its proof. The left-hand side is

(3.1) $$ \begin{align} &\sum_{i=0}^{{(n-(d-1))}/{d}} \sum_{j=0}^{{(n-(d-1))}/{d}}\dfrac{(q^{2d-2};q^{2d})_{i+j}(q^{d-1};q^{2d})_{i}(q^{d-1};q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{3di-i+2dj+2d-4} \notag \\[5pt] &\qquad\equiv \sum_{0 \le i+j \le {2(n-(d-1))}/{d}}^{} \dfrac{(q^{2d-2};q^{2d})_{i+j}(q^{d-1};q^{2d})_{i}(q^{d-1};q^{2d})_{j}}{(q^{2d};q^{2d})_{i+j}(q^{2d};q^{2d})_{i}(q^{2d};q^{2d})_{j}}q^{3di-i+2dj+2d-4} \notag\\[5pt] &\qquad\equiv \sum_{m=0}^{{2(n-(d-1))}/{d} } \begin{bmatrix} -\dfrac{d-1}{d} \\ m \end{bmatrix}_{q^ {2d}}\sum_{k=0}^{m} \begin{bmatrix} -\dfrac{d-1}{2d} \\ k \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{d-1}{2d} \\ m-k \end{bmatrix}_{q^{2d}}\notag\\[5pt]&\quad\qquad \times q^{(3d-3)m+(d-1)i+2dk^{2}-2dmk+2dm^{2}+2d-4}\notag\\[5pt] &\qquad \equiv \sum_{m=0}^{{2(n-(d-1))}/{d} } \begin{bmatrix} -\dfrac{d-1}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{d-1}{d} \\ m \end{bmatrix}_{q^{2d}}q^{4dm-4m+2dm^{2}+2d-4} \notag\\[5pt] &\qquad \equiv \sum_{m=0}^{{(n-(d-1))}/{d} } \begin{bmatrix} -\dfrac{d-1}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{d-1}{d} \\ m \end{bmatrix}_{q^{2d}}q^{4dm-4m+2dm^{2}+2d-4} \pmod{\Phi_n(q)^{2}}. \end{align} $$

To simplify this expression, note that

$$ \begin{align*} &\begin{bmatrix} -\dfrac{d-1}{d} _{} \\ m \end{bmatrix}_{q^{2d}}\begin{bmatrix} -\dfrac{d-1}{d} _{} \\ m \end{bmatrix}_{q^{2d}}\\ &\quad\equiv (-1)^{m} \begin{bmatrix} \dfrac{n-(d-1)}{d} _{} \\ m \end{bmatrix}_{q^{2d}}\begin{bmatrix} \dfrac{n-1}{d}+m _{} \\ m \end{bmatrix}_{q^{2d}} q^{-2nm-dm^{2}-dm+2m} \pmod{\Phi_n(q)^{2}}. \end{align*} $$

So the right-hand side of (3.1) becomes

$$ \begin{align*} &\sum_{m=0}^{{(n-(d-1))}/{d} } (-1)^{m} \begin{bmatrix} \dfrac{n-(d-1)}{d} \\ m \end{bmatrix}_{q^{2d}} \begin{bmatrix} \dfrac{n-1}{d} +m \\ m \end{bmatrix}_{q^{2d}}q^{(3d-2-2n)m+dm^{2}+2d-4}\\ &\qquad\equiv \sum_{m=0}^{{(n-(d-1))}{d} } \begin{bmatrix} \dfrac{n-(d-1)}{d} \\[2mm] \dfrac{n-(d-1)}{d}-m \end{bmatrix}_{q^{2d}} \begin{bmatrix} -\dfrac{n-1}{d}-1 \\[2mm] m \end{bmatrix}_{q^{2d}}q^{2dm^{2}+4(d-1)m}\\[1mm] &\qquad \equiv \begin{bmatrix} \dfrac{2}{d} -2 \\ \dfrac{n-(d-1)}{d} \end{bmatrix}_{q^{2d}}q^{{(2n^{2}-2)}{d}} \pmod{\Phi_n(q)^{2}}. \end{align*} $$

We can then complete the proof of Theorem 1.3 with the help of the q-Chu–Vandermonde identity (1.3).