No CrossRef data available.
Article contents
A NEW HIGHER ORDER YANG–MILLS–HIGGS FLOW ON RIEMANNIAN 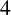 $4$-MANIFOLDS
$4$-MANIFOLDS
Published online by Cambridge University Press: 29 November 2022
Abstract
Let
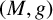 $(M,g)$
be a closed Riemannian
$(M,g)$
be a closed Riemannian
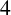 $4$
-manifold and let E be a vector bundle over M with structure group G, where G is a compact Lie group. We consider a new higher order Yang–Mills–Higgs functional, in which the Higgs field is a section of
$4$
-manifold and let E be a vector bundle over M with structure group G, where G is a compact Lie group. We consider a new higher order Yang–Mills–Higgs functional, in which the Higgs field is a section of
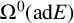 $\Omega ^0(\text {ad}E)$
. We show that, under suitable conditions, solutions to the gradient flow do not hit any finite time singularities. In the case that E is a line bundle, we are able to use a different blow-up procedure and obtain an improvement of the long-time result of Zhang [‘Gradient flows of higher order Yang–Mills–Higgs functionals’, J. Aust. Math. Soc. 113 (2022), 257–287]. The proof relies on properties of the Green function, which is very different from the previous techniques.
$\Omega ^0(\text {ad}E)$
. We show that, under suitable conditions, solutions to the gradient flow do not hit any finite time singularities. In the case that E is a line bundle, we are able to use a different blow-up procedure and obtain an improvement of the long-time result of Zhang [‘Gradient flows of higher order Yang–Mills–Higgs functionals’, J. Aust. Math. Soc. 113 (2022), 257–287]. The proof relies on properties of the Green function, which is very different from the previous techniques.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The second and third authors are partially supported by the National Key R and D Program of China 2020YFA0713100 and the Natural Science Foundation of China (Grant Numbers 12141104 and 11721101). The first author is supported by the Australian Research Council via grant FL170100020. The second author is funded by the China Postdoctoral Science Foundation (Grant Number 2022M713057). The third author is supported by the Natural Science Foundation of China (Grant Number 12201001), the Natural Science Foundation of Anhui Province (Grant Number 2108085QA17) and the Natural Science Foundation of Universities of Anhui Province (Grant Number KJ2020A0009).



