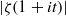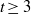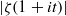Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dudek, Adrian W.
2015.
An explicit result for $|L(1+it,\chi)|$.
Functiones et Approximatio Commentarii Mathematici,
Vol. 53,
Issue. 1,
Trudgian, Tim
2016.
Improvements to Turing's method II.
Rocky Mountain Journal of Mathematics,
Vol. 46,
Issue. 1,
Hasanalizade, Elchin
Shen, Quanli
and
Wong, Peng-Jie
2022.
Counting zeros of the Riemann zeta function.
Journal of Number Theory,
Vol. 235,
Issue. ,
p.
219.
Simonič, Aleksander
2022.
Explicit Estimates for ζ(s) in the Critical Strip Under the Riemann Hypothesis.
The Quarterly Journal of Mathematics,
Vol. 73,
Issue. 3,
p.
1055.
Patel, Dhir
2022.
An explicit upper bound for |ζ(1+it)|.
Indagationes Mathematicae,
Vol. 33,
Issue. 5,
p.
1012.
Simonič, Aleksander
2023.
Estimates for L-functions in the Critical Strip Under GRH with Effective Applications.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 2,
Fiori, Andrew
Kadiri, Habiba
and
Swidinsky, Joshua
2023.
Sharper bounds for the Chebyshev function ψ(x).
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 2,
p.
127426.
Yang, Andrew
2024.
Explicit bounds on ζ(s) in the critical strip and a zero-free region.
Journal of Mathematical Analysis and Applications,
Vol. 534,
Issue. 2,
p.
128124.