Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gintz, Michael
Kortje, Matthew
Laurence, Megan
Liu, Yang
Wang, Zili
and
Yang, Yong
2022.
On the characterization of some non-abelian simple groups with few codegrees.
Communications in Algebra,
Vol. 50,
Issue. 9,
p.
3932.
Ahanjideh, Neda
2022.
Co-degree Graphs and Order Elements.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 5,
p.
2653.
Ahanjideh, Neda
2023.
Finite groups admitting at most two irreducible characters having equal co-degrees.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 04,
Yang, Yong
2023.
A characterization of the simple Ree groups 2𝐹4(𝑞2) by their character codegrees.
Journal of Group Theory,
Vol. 0,
Issue. 0,
Liu, Yang
and
Yang, Yong
2023.
Huppert’s Analogue Conjecture for $$ {\text{ PSL }}(3,q)$$ and $$ {\text{ PSU }}(3,q)$$.
Results in Mathematics,
Vol. 78,
Issue. 1,
Bahramian, Roya
Ahanjideh, Neda
and
Naghipour, Ali Reza
2023.
Groups with some cube-free irreducible character co-degrees.
Communications in Algebra,
Vol. 51,
Issue. 4,
p.
1772.
Ghasemi, Mohsen
and
Hekmatara, Somayeh
2023.
Equivalent version of Huppert’s conjecture for codegrees of K3-groups.
Quaestiones Mathematicae,
Vol. 46,
Issue. 9,
p.
1863.
GUAN, HAIYAN
ZHANG, XUNING
and
YANG, YONG
2023.
RECOGNISING REE GROUPS USING THE CODEGREE SET.
Bulletin of the Australian Mathematical Society,
Vol. 108,
Issue. 1,
p.
125.
DOLORFINO, MALLORY
MARTIN, LUKE
SLONIM, ZACHARY
SUN, YUXUAN
and
YANG, YONG
2024.
ON THE CHARACTERISATION OF SPORADIC SIMPLE GROUPS BY CODEGREES.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 1,
p.
57.
Wang, Hongning
Zhang, Xuning
Zhang, Selina
and
Chen, Michelle
2024.
On the characterization of some non-abelian simple groups using codegree set.
Communications in Algebra,
Vol. 52,
Issue. 3,
p.
1336.
DOLORFINO, MALLORY
MARTIN, LUKE
SLONIM, ZACHARY
SUN, YUXUAN
and
YANG, YONG
2024.
ON THE CHARACTERISATION OF ALTERNATING GROUPS BY CODEGREES.
Bulletin of the Australian Mathematical Society,
Vol. 110,
Issue. 1,
p.
115.
Gao, Li
Wang, Zhongbi
and
Chen, Guiyun
2024.
Finite groups with gcd(χ(1), χc
(1)) a prime.
Open Mathematics,
Vol. 22,
Issue. 1,
Bahramian, Roya
Ahanjideh, Neda
and
Naghipour, Ali Reza
2024.
The character co-degree sets and solvability.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 06,
Hung, Nguyen N
and
Moretó, Alexander
2024.
The codegree isomorphism problem for finite simple groups.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
1157.
Hung, Nguyen N
and
Moretó, Alexander
2025.
The codegree isomorphism problem for finite simple groups II.
The Quarterly Journal of Mathematics,
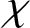 $\chi $
of a finite group G, the number
$\chi $
of a finite group G, the number
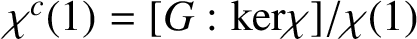 $\chi ^c(1)={[G:{\textrm {ker}}\chi ]}/{\chi (1)}$
is called the co-degree of
$\chi ^c(1)={[G:{\textrm {ker}}\chi ]}/{\chi (1)}$
is called the co-degree of
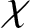 $\chi $
. A finite group G is an
$\chi $
. A finite group G is an
 ${\textrm {NDAC}} $
-group (no divisibility among co-degrees) when
${\textrm {NDAC}} $
-group (no divisibility among co-degrees) when
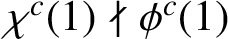 $\chi ^c(1) \nmid \phi ^c(1)$
for all irreducible characters
$\chi ^c(1) \nmid \phi ^c(1)$
for all irreducible characters
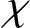 $\chi $
and
$\chi $
and
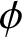 $\phi $
of G with
$\phi $
of G with
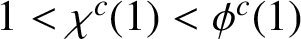 $1< \chi ^c(1) < \phi ^c(1)$
. We study finite groups admitting an irreducible character whose co-degree is a given prime p and finite nonsolvable
$1< \chi ^c(1) < \phi ^c(1)$
. We study finite groups admitting an irreducible character whose co-degree is a given prime p and finite nonsolvable
 ${\textrm {NDAC}} $
-groups. Then we show that the finite simple groups
${\textrm {NDAC}} $
-groups. Then we show that the finite simple groups
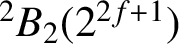 $^2B_2(2^{2f+1})$
, where
$^2B_2(2^{2f+1})$
, where
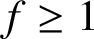 $f\geq 1$
,
$f\geq 1$
,
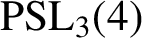 $\mbox {PSL}_3(4)$
,
$\mbox {PSL}_3(4)$
,
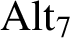 ${\textrm {Alt}}_7$
and
${\textrm {Alt}}_7$
and
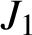 $J_1$
are determined uniquely by the set of their irreducible character co-degrees.
$J_1$
are determined uniquely by the set of their irreducible character co-degrees.


