Article contents
NONEXISTENCE OF A CIRCULANT EXPANDER FAMILY
Published online by Cambridge University Press: 17 November 2010
Abstract
The expansion constant of a simple graph G of order n is defined as 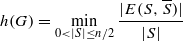 where
where 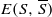 denotes the set of edges in G between the vertex subset S and its complement
denotes the set of edges in G between the vertex subset S and its complement 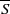 . An expander family is a sequence {Gi} of d-regular graphs of increasing order such that h(Gi)>ϵ for some fixed ϵ>0. Existence of such families is known in the literature, but explicit construction is nontrivial. A folklore theorem states that there is no expander family of circulant graphs only. In this note, we provide an elementary proof of this fact by first estimating the second largest eigenvalue of a circulant graph, and then employing Cheeger’s inequalities
. An expander family is a sequence {Gi} of d-regular graphs of increasing order such that h(Gi)>ϵ for some fixed ϵ>0. Existence of such families is known in the literature, but explicit construction is nontrivial. A folklore theorem states that there is no expander family of circulant graphs only. In this note, we provide an elementary proof of this fact by first estimating the second largest eigenvalue of a circulant graph, and then employing Cheeger’s inequalities 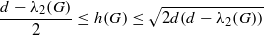 where G is a d-regular graph and λ2(G) denotes the second largest eigenvalue of G. Moreover, the associated equality cases are discussed.
where G is a d-regular graph and λ2(G) denotes the second largest eigenvalue of G. Moreover, the associated equality cases are discussed.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Publishing Association Inc. 2010
References
- 1
- Cited by


