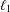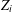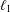Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Angosto, Carlos
Kadets, Vladimir
and
Zavarzina, Olesia
2019.
Non-expansive bijections, uniformities and polyhedral faces.
Journal of Mathematical Analysis and Applications,
Vol. 471,
Issue. 1-2,
p.
38.
Leo, Nikita
2022.
Plasticity of the unit ball of c and c0.
Journal of Mathematical Analysis and Applications,
Vol. 507,
Issue. 1,
p.
125718.
Karpenko, I.
and
Zavarzina, O.
2022.
Linear expand-contract plasticity of ellipsoids revisited.
Matematychni Studii,
Vol. 57,
Issue. 2,
p.
192.
Fakhoury, Micheline
2024.
Plasticity of the unit ball of some C(K) spaces.
Journal of Mathematical Analysis and Applications,
Vol. 530,
Issue. 2,
p.
127688.
Langemann, Dirk
and
Zavarzina, Olesia
2024.
Expand-contract plasticity on the real line.
Frontiers in Applied Mathematics and Statistics,
Vol. 10,
Issue. ,
Kurik, Kaarel August
2025.
Conditional plasticity of the unit ball of the ℓ∞-sum of finitely many strictly convex Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 541,
Issue. 2,
p.
128733.
Barroso, C. S.
2025.
$$\ell _1$$ spreading models and the FPP for Cesàro mean nonexpansive maps.
Banach Journal of Mathematical Analysis,
Vol. 19,
Issue. 2,