No CrossRef data available.
Published online by Cambridge University Press: 08 October 2024
Let p be a prime number. Let 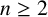 $n\geq 2$ be an integer given by
$n\geq 2$ be an integer given by 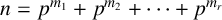 $n = p^{m_1} + p^{m_2} + \cdots + p^{m_r}$, where
$n = p^{m_1} + p^{m_2} + \cdots + p^{m_r}$, where 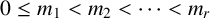 $0\leq m_1 < m_2 < \cdots < m_r$ are integers. Let
$0\leq m_1 < m_2 < \cdots < m_r$ are integers. Let  $a_0, a_1, \ldots , a_{n-1}$ be integers not divisible by p. Let
$a_0, a_1, \ldots , a_{n-1}$ be integers not divisible by p. Let 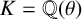 $K = \mathbb Q(\theta )$ be an algebraic number field with
$K = \mathbb Q(\theta )$ be an algebraic number field with 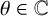 $\theta \in {\mathbb C}$ a root of an irreducible polynomial
$\theta \in {\mathbb C}$ a root of an irreducible polynomial 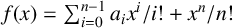 $f(x) = \sum _{i=0}^{n-1}a_i{x^i}/{i!} + {x^n}/{n!}$ over the field
$f(x) = \sum _{i=0}^{n-1}a_i{x^i}/{i!} + {x^n}/{n!}$ over the field  $\mathbb Q$ of rationals. We prove that p divides the common index divisor of K if and only if
$\mathbb Q$ of rationals. We prove that p divides the common index divisor of K if and only if 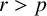 $r>p$. In particular, if
$r>p$. In particular, if 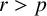 $r>p$, then K is always nonmonogenic. As an application, we show that if
$r>p$, then K is always nonmonogenic. As an application, we show that if 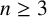 $n \geq 3$ is an odd integer such that
$n \geq 3$ is an odd integer such that 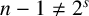 $n-1\neq 2^s$ for
$n-1\neq 2^s$ for 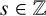 $s\in {\mathbb Z}$ and K is a number field generated by a root of a truncated exponential Taylor polynomial of degree n, then K is always nonmonogenic.
$s\in {\mathbb Z}$ and K is a number field generated by a root of a truncated exponential Taylor polynomial of degree n, then K is always nonmonogenic.
Dedicated to Professor Sudesh K. Khanduja on her 74th birthday
The author is thankful to the Indian Institute of Technology, Madras for NFIG grant RF/22-23/1035/MA/NFIG/009034.