Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harman, C.J.
1974.
A note on a discrete analytic function.
Bulletin of the Australian Mathematical Society,
Vol. 10,
Issue. 1,
p.
123.
Harman, C.J.
1974.
A new definition of discrete analytic functions.
Bulletin of the Australian Mathematical Society,
Vol. 10,
Issue. 2,
p.
281.
Harman, C. J.
and
Duffin, R. J.
1979.
Discrete geometric function theory II.
Applicable Analysis,
Vol. 9,
Issue. 3,
p.
191.
Harman, C.J
1981.
Discrete analysis on a radial lattice.
Journal of Mathematical Analysis and Applications,
Vol. 79,
Issue. 2,
p.
323.
Alpay, Daniel
Jorgensen, Palle
Seager, Ron
and
Volok, Dan
2013.
On discrete analytic functions: Products, rational functions and reproducing kernels.
Journal of Applied Mathematics and Computing,
Vol. 41,
Issue. 1-2,
p.
393.
Alpay, Daniel
and
Volok, Dan
2023.
Schur analysis and discrete analytic functions: Rational functions and co-isometric realizations.
Linear Algebra and its Applications,
Vol. 675,
Issue. ,
p.
179.


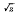 . An analogue
. An analogue 