No CrossRef data available.
Published online by Cambridge University Press: 17 April 2009
Consider the first order differential equation (1) 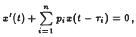 , where pi, and τi, for i = 1,…,n, are positive constants. To find necessary and sufficient conditions, in terms of the coefficients and the delays only, under which all solutions of (1) oscillate, is a problem of great importence. In a recent paper, Bowcock and Yu claimed that
, where pi, and τi, for i = 1,…,n, are positive constants. To find necessary and sufficient conditions, in terms of the coefficients and the delays only, under which all solutions of (1) oscillate, is a problem of great importence. In a recent paper, Bowcock and Yu claimed that 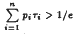 is a necessary and sufficient condition for all solutions of (1) to be oscillatory. In this paper a counterexample shows that the above result is not valid and the error in this paper is indicated.
is a necessary and sufficient condition for all solutions of (1) to be oscillatory. In this paper a counterexample shows that the above result is not valid and the error in this paper is indicated.
 oscillate’, J. Differential Equations 53 (1984), 139–145.Google Scholar
oscillate’, J. Differential Equations 53 (1984), 139–145.Google Scholar