No CrossRef data available.
Article contents
A note on connected submetaLindelöf spaces
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we shall show that if m is a natural number and for every 0 ≦ n ≦ m, 
 and 2ω ≦ ωm are assumed, then connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω are Lindelöf. Furthermore, we shall show that
and 2ω ≦ ωm are assumed, then connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω are Lindelöf. Furthermore, we shall show that 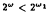 if and only if connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω and tightness ≦ ω are Lindelöf.
if and only if connected, locally Lindelöf, submetaLindelöf, normal spaces of character ≦ 2ω and tightness ≦ ω are Lindelöf.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1989
References
[1]Balogh, Z., ‘Paracompactness in locally Lindelöf spaces.’, Caned. J. Math. 38 (1986), 719–727.CrossRefGoogle Scholar
[2]Charlesworth, A., Hodel, R. and Tall, F.D., ‘On a theorem of Jones and Heath concerning discrete subspaces’, Colloq. Math. 34 (1975), 33–37.CrossRefGoogle Scholar
[3]Devlin, K.J., Shelah, S., ‘A weak version of ◊ wnich follows  ’, Israel J. Math. 29 (1978), 239–247.CrossRefGoogle Scholar
’, Israel J. Math. 29 (1978), 239–247.CrossRefGoogle Scholar
[4]Engelking, R., Outline of General Topology (Polish Scientific Publishers, Warszawa, 1965).Google Scholar
[7]Taylor, A.D., ‘Diamond principles, ideals and the normal Moore problem’, Canad. J. Math. 33 (1981), 282–296.CrossRefGoogle Scholar

